Chat with AIExam 8: Mathematical Modeling With Differential Equations
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
State the order of the differential equation, and decide which family of functions is a solution.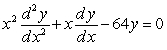 
(Multiple Choice)
4.9/5 
(37)
(37) Use Euler's method with the step size of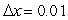 
to compute the approximate solution to the initial-valued problem 
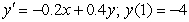at 
. Round your answer to six decimal places if need be.
to compute the approximate solution to the initial-valued problem at 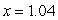. Round your answer to six decimal places if need be. (Short Answer)
4.9/5 (29)
(29) Suppose 5 grams of a radioactive substance decays according to the equation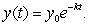 
If it takes 
years for the substance to reduce to 
of its original mass, write an equation for the amount of the substance present as a function of time.
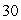If it takes years for the substance to reduce to 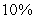of its original mass, write an equation for the amount of the substance present as a function of time. (Short Answer)
4.9/5 (30)
(30) 
A certain radioactive substance has a half-life of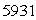 
years. Approximately how many years will it take so that only 
of the original amount remains? Round your answers to six decimal places.
years. Approximately how many years will it take so that only 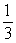of the original amount remains? Round your answers to six decimal places. (Short Answer)
4.9/5 (28)
(28) What is the solution to the following differential equation?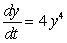 
(Multiple Choice)
4.8/5 (34)
(34) A cup of water with a temperature of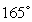 
C is placed in a room at constant temperature 
C. It takes 
minutes for the cup to cool to 
. Assuming Newton's Law of Cooling applies, find the temperature, T, of the cup of water at any time t. Express all numerical quantities in exact form.
C is placed in a room at constant temperature 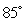C. It takes 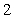minutes for the cup to cool to 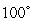. Assuming Newton's Law of Cooling applies, find the temperature, T, of the cup of water at any time t. Express all numerical quantities in exact form. (Short Answer)
4.9/5 (36)
(36) 
the situation modeled is
What is the solution to the following differential equation?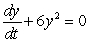 
(Multiple Choice)
4.9/5 (40)
(40) A particle moving along the x-axis encounters a resisting force that results in an acceleration of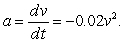 
Given that 
cm and v = 35 cm/s at t = 0, find the position x as a function of t.
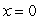Given that cm and v = 35 cm/s at t = 0, find the position x as a function of t. (Short Answer)
4.8/5 (34)
(34) Use Euler's method with the step size of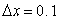 
to approximate solution to the initial-value problem 
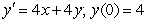at 
.
to approximate solution to the initial-value problem at 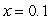. (Multiple Choice)
4.8/5 (32)
(32) What is the solution to the following initial-value problem? (Use separation of variables!)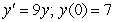 
(Multiple Choice)
4.9/5 (41)
(41) A tank is filled with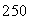 
gallons of water with 
oz of salt dissolved in it. At t = 0, salt solution containing 
oz/gal enters the tank at a rate of 
gal/min. Well-mixed solution leaves at the same rate. Write down an expression that gives the amount of salt S, in the tank at any time t.
gallons of water with 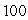oz of salt dissolved in it. At t = 0, salt solution containing 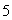oz/gal enters the tank at a rate of 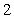gal/min. Well-mixed solution leaves at the same rate. Write down an expression that gives the amount of salt S, in the tank at any time t. (Short Answer)
4.8/5 (36)
(36) Suppose that an initial population of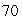 
bacteria grows exponentially at a rate of 
% per hour. How many bacteria are present after t hours?
bacteria grows exponentially at a rate of 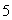% per hour. How many bacteria are present after t hours? (Multiple Choice)
4.8/5 (34)
(34) A tank is filled with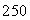 
gallons of water in which 
oz of salt is dissolved. At t = 0, salt solution containing 
oz/gal enters the tank at a rate of 
gal/min. Well mixed solution leaves at the same rate. Write down an expression that gives the amount of salt S, in the tank at any time t.
gallons of water in which 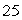oz of salt is dissolved. At t = 0, salt solution containing 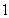oz/gal enters the tank at a rate of 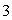gal/min. Well mixed solution leaves at the same rate. Write down an expression that gives the amount of salt S, in the tank at any time t. (Short Answer)
4.8/5 (40)
(40) What is the solution to the following differential equation? (Use separation of variables!)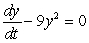 
(Multiple Choice)
4.8/5 (33)
(33) A cup of water with a temperature of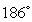 
C is placed in a room with constant temperature 
C. It takes 
minutes for the cup to cool to 
. Assuming Newton's Law of Cooling applies, find the temperature, T, of the cup of water at any time t. Express all numerical quantities in exact form.
C is placed in a room with constant temperature 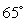C. It takes 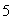minutes for the cup to cool to 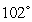. Assuming Newton's Law of Cooling applies, find the temperature, T, of the cup of water at any time t. Express all numerical quantities in exact form. (Short Answer)
4.7/5 (30)
(30) 
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)