Exam 14: Multiple Integrals
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
The equation of the tangent plane to x = u, y = v, 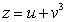 where u = 1 and v = 0 is
where u = 1 and v = 0 is
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
E
Find the volume of the solid bounded by ![Find the volume of the solid bounded by and the rectangle R = [0, 3] *[0, 3].](https://storage.examlex.com/TB6988/11ead0bc_8dab_b1a5_99a0_7b2250c5e2e9_TB6988_11.jpg) and the rectangle R = [0, 3] *[0, 3].
and the rectangle R = [0, 3] *[0, 3].
Free
(Multiple Choice)
4.8/5  (27)
(27)
Correct Answer:
E
Find the Jacobian if u = 2xy and v = 2x + 6.
Free
(Multiple Choice)
4.8/5  (43)
(43)
Correct Answer:
D
Use a double integral in polar coordinates to find the volume of the solid enclosed by x2 + y2 = 40 - z and z = 4.
(Essay)
4.7/5  (41)
(41)
Find the mass of the tetrahedron in the first octant enclosed by the coordinate planes and the plane x + y + z = 1 if its density is given by (x, y, z) = 11xy.
(Essay)
4.8/5  (37)
(37)
Use the theorem of Pappas to find the volume of the solid generated when the region enclosed by y = 3x2 and y = 3(8 - x2) is revolved about the line y = -2.
Obtain the centroid by symmetry.
(Essay)
4.8/5  (42)
(42)
Evaluate 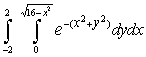 by converting to an equivalent integral in polar coordinates. Sketch the region R.
by converting to an equivalent integral in polar coordinates. Sketch the region R.
(Essay)
4.8/5  (27)
(27)
Find 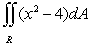 where R is the region in the first quadrant enclosed between y = x and y = x5.
where R is the region in the first quadrant enclosed between y = x and y = x5.
(Multiple Choice)
5.0/5  (37)
(37)
Use a double integral in polar coordinates to find the volume that is inside the sphere x2 + y2 + z2 = 16, outside the cylinder x2 + y2 = 4 and above z = 0.
(Essay)
4.7/5  (26)
(26)
Find the volume of the region bounded above by the plane 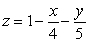 in the first octant.
in the first octant.
(Multiple Choice)
4.8/5  (38)
(38)
A lamina with density (x, y) = 2x2 + y2 + 9 is bounded by x = y, x = 0, y = 0, y = 2. Find its center of mass.
(Multiple Choice)
4.9/5  (30)
(30)
Find the volume of the solid in the first octant enclosed by z = 3(4 - y2), z = 0, x = 0, y = x, and y = 2.
(Short Answer)
4.9/5  (35)
(35)
Find the volume of the solid enclosed by y = x2 - x + a, y = x + a, z = x + 1, and the xy-plane.
(Essay)
4.9/5  (42)
(42)
Use an appropriate transform to evaluate 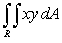 where R is the region enclosed by
where R is the region enclosed by 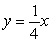 ,
, 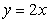 , and
, and 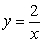 .
.
(Essay)
4.7/5  (43)
(43)
Use a triple integral to find the volume of the solid in the first octant enclosed by the cylinder x = 4 - y2 and the planes z = y, x = 0, and z = 0.
(Essay)
4.8/5  (43)
(43)
A lamina with density (x, y) = 2x2 + y2 is bounded by x = y, x = 0, y = 0, y = 2. Find its moment of inertia about the y-axis.
(Multiple Choice)
4.7/5  (35)
(35)
Showing 1 - 20 of 117
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)