Exam 7: Principle of Integral Evaluation
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Use n = 10 subdivisions to approximate the value of the integral 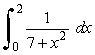 by Simpson's rule.
by Simpson's rule.
(Short Answer)
4.9/5  (35)
(35)
Use the trapezoid rule with n = 10 to approximate the integral. 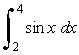
(Multiple Choice)
4.9/5  (36)
(36)
Use the trapezoid rule with n = 10 to approximate the integral. 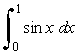
(Short Answer)
4.8/5  (30)
(30)
Use n = 10 subdivisions to find the exact value of 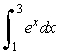 by the trapezoidal approximation. Find the exact value of the integral and approximate the magnitude of the error. Express your answer to at least four decimal places.
by the trapezoidal approximation. Find the exact value of the integral and approximate the magnitude of the error. Express your answer to at least four decimal places.
(Short Answer)
4.8/5  (46)
(46)
Use the trapezoid rule with n = 10 to approximate the integral. 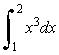
(Short Answer)
4.8/5  (32)
(32)
Showing 41 - 60 of 269
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)