Exam 2: The Derivative
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Find the value of the constant A in y = A sin 3t so that d2y/dt2 + 7y = sin 3t.
(Multiple Choice)
4.8/5  (26)
(26)
Find equations for the tangents and normals to the graph of y = 30 - x - x2 at the points where the curve intersects the x-axis.
(Essay)
4.9/5  (35)
(35)
Let ![Let . Find the average rate of change of y with respect to x over the interval [4,7].](https://storage.examlex.com/TB6988/11ead0bc_8d7b_a15c_99a0_41f54bc3ad81_TB6988_11.jpg) . Find the average rate of change of y with respect to x over the interval [4,7].
. Find the average rate of change of y with respect to x over the interval [4,7].
(Essay)
4.9/5  (40)
(40)
Given that f(1) = 5 and f '(1) = 6, find an equation for the tangent line to the graph of y = f(x) at the point where x = 1.
(Short Answer)
4.8/5  (40)
(40)
Let f(x) = ax3 + b, where a and b are constants. Use the method of Section 3.1 to show that the slope of the tangent to the graph of f at x = x0 is 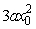 .
.
(Essay)
4.9/5  (28)
(28)
Showing 21 - 40 of 198
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)