Exam 12: Vector-Valued Functions
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
Find the speed of a particle moving along the curve r(t) = (13 + t3)i + 4t j - t2 k at t = 1.
(Multiple Choice)
4.8/5  (24)
(24)
Sketch x = 2 cos t, y = 3 sin t for 0 t 2 . Calculate the radius of curvature at 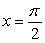 and sketch the oscillating circle.
and sketch the oscillating circle.
(Essay)
4.9/5  (45)
(45)
Find the parametric equations that correspond to the given vector equation: 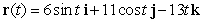 .
.
(Multiple Choice)
4.8/5  (38)
(38)
Find the acceleration of a particle moving along the curve r(t) = t3 i + (8 + 4t)j - t2 k at t = 1.
(Multiple Choice)
4.8/5  (37)
(37)
Find the curvature 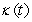 for r(t) = 17i + 2t j + 3t2 k at t = 0.
for r(t) = 17i + 2t j + 3t2 k at t = 0.
(Multiple Choice)
4.7/5  (41)
(41)
Find the arc length parameterization of the line 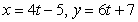 that has the same orientation as the given curve and uses
that has the same orientation as the given curve and uses 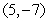 as a reference point.
as a reference point.
(Multiple Choice)
4.8/5  (36)
(36)
Let r(t) = (-9 + t) i + t2 j + t3 k. Find T(t) when t = 0.
(Multiple Choice)
4.9/5  (38)
(38)
Find the unit tangent and unit normal vectors to r(t) = t i + ln(cos t) j at 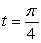 .
.
(Essay)
4.8/5  (37)
(37)
Find the unit tangent and unit normal vectors to the curve r(t) = 2 sin t i + 3 cos t j at 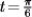 . Sketch a portion of the curve showing the point of tangency.
. Sketch a portion of the curve showing the point of tangency.
(Essay)
4.8/5  (34)
(34)
Let r(t) = (t2 + 2)i + e t j + (9 + e t )k. Find T(t) for t = 0.
(Multiple Choice)
4.9/5  (23)
(23)
Find the speed of a particle in a circular orbit with radius 1022m around an object of mass 1023kg. (G = 6.67 *10-11m/kg·s2)
(Multiple Choice)
5.0/5  (34)
(34)
Showing 101 - 120 of 147
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)