Exam 7: Introduction to Risk and Return
Exam 1: Introduction to Corporate Finance49 Questions
Exam 2: How to Calculate Present Values100 Questions
Exam 3: Valuing Bonds62 Questions
Exam 4: The Value of Common Stocks65 Questions
Exam 5: Net Present Value and Other Investment Criteria74 Questions
Exam 6: Making Investment Decisions With the Net Present Value Rule75 Questions
Exam 7: Introduction to Risk and Return90 Questions
Exam 8: Portfolio Theory and the Capital Asset Pricing Model89 Questions
Exam 9: Risk and the Cost of Capital76 Questions
Exam 10: Project Analysis69 Questions
Exam 11: How to Ensure That Projects Truly Have Positive Npvs71 Questions
Exam 12: Agency Problems and Investment67 Questions
Exam 13: Efficient Markets and Behavioral Finance58 Questions
Exam 14: An Overview of Corporate Financing61 Questions
Exam 15: How Corporations Issue Securities69 Questions
Exam 16: Payout Policy70 Questions
Exam 17: Does Debt Policy Matter78 Questions
Exam 18: How Much Should a Corporation Borrow75 Questions
Exam 19: Financing and Valuation83 Questions
Exam 20: Understanding Options76 Questions
Exam 21: Valuing Options75 Questions
Exam 22: Real Options58 Questions
Exam 23: Credit Risk and the Value of Corporate Debt53 Questions
Exam 24: The Many Different Kinds of Debt100 Questions
Exam 25: Leasing54 Questions
Exam 26: Managing Risk67 Questions
Exam 27: Managing International Risks64 Questions
Exam 28: Financial Analysis52 Questions
Exam 29: Financial Planning59 Questions
Exam 30: Working Capital Management86 Questions
Exam 31: Mergers78 Questions
Exam 32: Corporate Restructuring70 Questions
Exam 33: Governance and Corporate Control Around the World50 Questions
Select questions type
The correlation coefficient between stock B and the market portfolio is 0.8. The standard deviation of stock B is 35 percent and that of the market is 20 percent. Calculate the beta of the stock.
(Multiple Choice)
4.7/5  (39)
(39)
If the correlation coefficient between the returns on stock C and stock D is +1.0, the standard deviation of return for stock C is 15 percent, and that for stock D is 30 percent, calculate the covariance between stock C and stock D.
(Multiple Choice)
4.8/5  (42)
(42)
What has been the approximate standard deviation of returns of U.S. common stocks during the period between 1900 and 2017?
(Multiple Choice)
4.8/5  (28)
(28)
Sun Corporation has had returns of -6 percent, 16 percent, 18 percent, and 28 percent for the past four years. Calculate the standard deviation of the returns using the correction for the loss of a degree of freedom shown below.
When variance is estimated from a sample of observed returns, we add the squared deviations and divide by N -1, where N is the number of observations. We divide by N -1 rather than N to correct for a loss of a degree of freedom. The formula is
Variance(  m )=
m )= 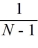
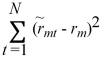 Where
Where  m is the market return in period t and rm is the mean of the values of rmt.
m is the market return in period t and rm is the mean of the values of rmt.
(Multiple Choice)
4.8/5  (33)
(33)
Diversification reduces the risk of a portfolio because the prices of different securities do not move exactly together.
(True/False)
4.7/5  (40)
(40)
For the most part, stock returns tend to move together. Thus, pairs of stocks tend to have both positive covariances and correlations.
(True/False)
4.8/5  (38)
(38)
One dollar invested in a portfolio of long-term U.S. government bonds in 1900 would have grown in nominal value by the end of year 2017 to:
(Multiple Choice)
4.8/5  (38)
(38)
Assume the following data: Risk-free rate = 4.0 percent; average risk premium = 7.7 percent. Calculate the required rate of return for the risky asset.
(Multiple Choice)
4.9/5  (38)
(38)
What has been the average annual real rate of interest on Treasury bills over the past 117 years (from 1900 to 2017)?
(Multiple Choice)
4.8/5  (36)
(36)
What has been the average annual nominal rate of interest on Treasury bills over the past 117 years (1900-2017)?
(Multiple Choice)
4.8/5  (33)
(33)
A stock having a covariance with the market that is higher than the variance of the market will always have a beta above 1.0.
(True/False)
4.8/5  (32)
(32)
Treasury bills typically provide higher average returns, both in nominal terms and in real terms, than long-term government bonds.
(True/False)
4.9/5  (34)
(34)
In the formula for calculating the variance of an N-stock portfolio, how many covariance and variance terms are there?
(Essay)
4.9/5  (36)
(36)
The portfolio risk that cannot be eliminated by diversification is called unique risk.
(True/False)
4.8/5  (35)
(35)
Macro Corporation has had the following returns for the past three years: -10 percent, 10 percent, and 30 percent. Use the following formulas to calculate the standard deviation of the returns:
Variance (  m)= expected value of (
m)= expected value of (  m - rm)2
Standard deviation of
m - rm)2
Standard deviation of  m =
m = 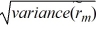 .
.
(Multiple Choice)
4.9/5  (43)
(43)
The annual returns for three years for stock B were 0 percent, 10 percent, and 26 percent. Annual returns for three years for the market portfolio were +6 percent, 18 percent, and 24 percent. Calculate the beta for the stock.
(Multiple Choice)
4.7/5  (34)
(34)
Which portfolio has had the highest average risk premium during the period 1900-2017?
(Multiple Choice)
5.0/5  (47)
(47)
Showing 61 - 80 of 90
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)