Exam 10: Regression Analysis: Estimating Relationships
Exam 1: Introduction to Business Analytics24 Questions
Exam 2: Describing the Distribution of a Variable73 Questions
Exam 3: Finding Relationships Among Variables56 Questions
Exam 4: Business Intelligence Bifor Data Analysis62 Questions
Exam 5: Probability and Probability Distributions132 Questions
Exam 6: Decision Making Under Uncertainty79 Questions
Exam 7: Sampling and Sampling Distributions78 Questions
Exam 8: Confidence Interval Estimation60 Questions
Exam 9: Hypothesis Testing70 Questions
Exam 10: Regression Analysis: Estimating Relationships80 Questions
Exam 11: Regression Analysis: Statistical Inference69 Questions
Exam 12: Time Series Analysis and Forecasting95 Questions
Exam 13: Introduction to Optimization Modeling70 Questions
Exam 14: Optimization Models87 Questions
Exam 15: Introduction to Simulation Modeling58 Questions
Exam 16: Simulation Models59 Questions
Exam 17: Data Mining30 Questions
Exam 18: Analysis of Variance and Experimental Design24 Questions
Exam 19: Statistical Process Control24 Questions
Select questions type
Correlation is used to determine the strength of the linear relationship between an explanatory variable X and response variable Y.
(True/False)
4.9/5  (34)
(34)
In a simple linear regression analysis,the following sums of squares are produced: 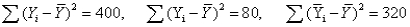 The proportion of the variation in Y that is explained by the variation in X is
The proportion of the variation in Y that is explained by the variation in X is
(Multiple Choice)
4.8/5  (35)
(35)
An interaction variable is the product of an explanatory variable and the dependent variable.
(True/False)
4.8/5  (36)
(36)
The residual is defined as the difference between the actual and predicted,or fitted values of the response variable.
(True/False)
4.9/5  (37)
(37)
The regression line 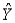 = 3 + 2X has been fitted to the data points (4,14),(2,7),and (1,4).The sum of the residuals squared will be 8.0.
= 3 + 2X has been fitted to the data points (4,14),(2,7),and (1,4).The sum of the residuals squared will be 8.0.
(True/False)
4.9/5  (40)
(40)
In a constant elasticity,or multiplicative,relationship the dependent variable is expressed as a product of explanatory variables raised to powers.
(True/False)
4.8/5  (37)
(37)
A scatterplot that appears as a shapeless mass of data points indicates _____ relationship among the variables.
(Multiple Choice)
4.9/5  (40)
(40)
In regression analysis,which of the following causal relationships are possible?
(Multiple Choice)
4.9/5  (28)
(28)
If a categorical variable is to be included in a multiple regression,a dummy variable for each category of the variable should be used,but the original categorical variables should not be used.
(True/False)
4.8/5  (41)
(41)
In reference to the equation, 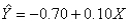 ,the value 0.10 is the expected change in Y per unit change in X.
,the value 0.10 is the expected change in Y per unit change in X.
(True/False)
5.0/5  (43)
(43)
A useful graph in almost any regression analysis is a scatterplot of residuals (on the vertical axis)versus fitted values (on the horizontal axis),where a "good" fit not only has small residuals,but it has residuals scattered randomly around zero with no apparent pattern.
(True/False)
4.8/5  (40)
(40)
A regression analysis between X = sales (in $1000s)and Y = advertising ($)resulted in the following least squares line: 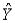 = 84 +7X.This implies that if advertising is $800,then the predicted amount of sales (in dollars)is $140,000.
= 84 +7X.This implies that if advertising is $800,then the predicted amount of sales (in dollars)is $140,000.
(True/False)
4.8/5  (31)
(31)
The effect of a logarithmic transformation on a variable that is skewed to the right by a few large values is to "squeeze" the values together and make the distribution more symmetric.
(True/False)
4.9/5  (24)
(24)
In a simple regression with a single explanatory variable,the multiple R is the same as the standard correlation between the Y variable and the explanatory X variable.
(True/False)
4.8/5  (31)
(31)
In a simple linear regression problem,if 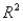 = 0.95,this means that 95% of the variation in the explanatory variable X can be explained by the regression.
= 0.95,this means that 95% of the variation in the explanatory variable X can be explained by the regression.
(True/False)
4.8/5  (33)
(33)
In simple linear regression,the divisor of the standard error of estimate 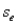 is n - 1,because there is only one explanatory variable.
is n - 1,because there is only one explanatory variable.
(True/False)
4.9/5  (28)
(28)
The two primary objectives of regression analysis are to study relationships between variables and to use those relationships to make predictions.
(True/False)
4.8/5  (37)
(37)
An important condition when interpreting the coefficient for a particular independent variable X in a multiple regression equation is that
(Multiple Choice)
4.8/5  (36)
(36)
Showing 21 - 40 of 80
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)