Exam 15: Oscillations
Exam 1: Measurement37 Questions
Exam 2: Motion Along a Straight Line90 Questions
Exam 3: Vector32 Questions
Exam 4: Motion in Two and Three Dimensions53 Questions
Exam 5: Force and Motion I73 Questions
Exam 6: Force and Motion II74 Questions
Exam 7: Kinetic Energy and Work72 Questions
Exam 8: Potential Energy and Conservation of Energy62 Questions
Exam 9: Center of Mass and Linear Momentum98 Questions
Exam 10: Rotation99 Questions
Exam 11: Rolling, Torque, and Angular Momentum65 Questions
Exam 12: Equilibrium and Elasticity57 Questions
Exam 13: Gravitation54 Questions
Exam 14: Fluids87 Questions
Exam 15: Oscillations75 Questions
Exam 16: Waves I80 Questions
Exam 17: Waves II70 Questions
Exam 18: Temperature, Heat, and the First Law of Thermodynamics96 Questions
Exam 19: The Kinetic Theory of Gases111 Questions
Exam 20: Entropy and the Second Law of Thermodynamics61 Questions
Exam 21: Electric Charge51 Questions
Exam 22: Electric Fields52 Questions
Exam 23: Gauss Law39 Questions
Exam 24: Electric Potential50 Questions
Exam 25: Capacitance59 Questions
Exam 26: Current and Resistance54 Questions
Exam 27: Circuits73 Questions
Exam 28: Magnetic Fields51 Questions
Exam 29: Magnetic Fields Due to Currents48 Questions
Exam 30: Induction and Inductance90 Questions
Exam 31: Electromagnetic Oscillations and Alternating Current86 Questions
Exam 32: Maxwells Equations; Magnetism of Matter81 Questions
Exam 33: Electromagnetic Waves81 Questions
Exam 34: Images78 Questions
Exam 35: Interference45 Questions
Exam 36: Diffraction77 Questions
Exam 37: Relativity68 Questions
Exam 38: Photons and Matter Waves57 Questions
Exam 39: More About Matter Waves41 Questions
Exam 40: All About Atoms76 Questions
Exam 41: Conduction of Electricity in Solids49 Questions
Exam 42: Nuclear Physics68 Questions
Exam 43: Energy From the Nucleus50 Questions
Exam 44: Quarks, Leptons, and the Big Bang55 Questions
Select questions type
The displacement of an object oscillating on a spring is given by x(t)= xmcos( t + ).If the initial displacement is zero and the initial velocity is in the negative x direction, then the phase constant is:
(Multiple Choice)
4.9/5  (32)
(32)
An oscillator is driven by a sinusoidal force.The frequency of the applied force:
(Multiple Choice)
4.8/5  (39)
(39)
A particle is in simple harmonic motion along the x axis.The amplitude of the motion is xm.When it is at x = x1, its kinetic energy is K = 5 J and its potential energy (measured with U = 0 at x = 0)is U = 3 J.When it is at x = -1/2 xm, the kinetic and potential energies are:
(Multiple Choice)
4.7/5  (47)
(47)
A particle undergoes damped harmonic motion.The spring constant is 100 N/m; the damping constant is 8.0 x 10-3 kg∙m/s, and the mass is 0.050 kg.If the particle starts at its maximum displacement, x = 1.5 m, at time t = 0, what is the angular frequency of the oscillations?
(Multiple Choice)
4.9/5  (28)
(28)
A particle is in simple harmonic motion with period T.At time t=0 it is halfway between the equilibrium point and an end point of its motion, travelling toward the end point.The next time it is at the same place is:
(Multiple Choice)
4.8/5  (32)
(32)
Three physical pendulums, with masses m1, m2 = 2m1, and m3 = 3m1, have the same shape and size and are suspended at the same point.Rank them according to their periods, from shortest to longest.
(Multiple Choice)
4.7/5  (35)
(35)
A simple pendulum consists of a small ball tied to a string and set in oscillation.As the pendulum swings the tension in the string is:
(Multiple Choice)
4.8/5  (38)
(38)
Two identical undamped oscillators have the same amplitude of oscillation only if:
(Multiple Choice)
4.8/5  (37)
(37)
A disk whose rotational inertia is 450 kg∙m2 hangs from a wire whose torsion constant is 2300 N∙m/rad.What is the angular frequency of its torsional oscillations?
(Multiple Choice)
4.8/5  (40)
(40)
A weight suspended from an ideal spring oscillates up and down with a period T.If the amplitude of the oscillation is doubled, the period will be:
(Multiple Choice)
4.9/5  (36)
(36)
Two uniform spheres are pivoted on horizontal axes that are tangent to their surfaces.The one with the longer period of oscillation is the one with:
(Multiple Choice)
4.8/5  (42)
(42)
This plot shows a mass oscillating as x = xm cos (ωt + φ).What are xm and φ? 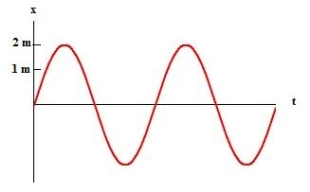
(Multiple Choice)
4.8/5  (42)
(42)
A sinusoidal force with a given amplitude is applied to an oscillator.At resonance the amplitude of the oscillation is limited by:
(Multiple Choice)
4.9/5  (38)
(38)
A particle is in simple harmonic motion along the x axis.The amplitude of the motion is xm.When it is at x = x1, its kinetic energy is K = 5 J and its potential energy (measured with U = 0 at x = 0)is U = 3 J.When its kinetic energy is 8 J, it is at:
(Multiple Choice)
4.7/5  (36)
(36)
An object is undergoing simple harmonic motion.Throughout a complete cycle it:
(Multiple Choice)
4.9/5  (32)
(32)
The displacement of an object oscillating on a spring is given by x(t)= xmcos( t + ).If the object is initially displaced in the negative x direction and given a negative initial velocity, then the phase constant is between:
(Multiple Choice)
4.9/5  (37)
(37)
Below are sets of values for the spring constant k, damping constant b, and mass m for a particle in damped harmonic motion.Which of the sets takes the longest time for its mechanical energy to decrease to one-fourth of its initial value? 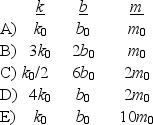
(Multiple Choice)
4.8/5  (42)
(42)
The rotational inertia of a uniform thin rod about its end is ML2/3, where M is the mass and L is the length.Such a rod is hung vertically from one end and set into small amplitude oscillation.If L = 1.0 m this rod will have the same period as a simple pendulum of length:
(Multiple Choice)
4.8/5  (34)
(34)
Let U be the potential energy (with the zero at zero displacement)and K be the kinetic energy of a simple harmonic oscillator.Uavg and Kavg are the average values over a cycle.Then:
(Multiple Choice)
4.9/5  (41)
(41)
Showing 21 - 40 of 75
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)