Exam 12: Markov Process Models
Exam 1: Introduction to Management Science Models50 Questions
Exam 2: Introduction to Management Science Models58 Questions
Exam 3: Applications of Linear and Integer Programming Models53 Questions
Exam 4: Network Models54 Questions
Exam 5: Project Scheduling Models55 Questions
Exam 6: Decision Models46 Questions
Exam 7: Forecasting49 Questions
Exam 8: Inventory Models54 Questions
Exam 9: Queuing Models54 Questions
Exam 10: Simulation Models54 Questions
Exam 11: Quality Management Models50 Questions
Exam 12: Markov Process Models49 Questions
Exam 13: Nonlinear Models:dynamic, Goal, and Nonlinear Programming53 Questions
Select questions type
In determining steady-state behavior for a process with absorbing states, the subdivision of the transition matrix yields:
(Multiple Choice)
4.9/5  (33)
(33)
A simple computer game using a Markov chain starts at the Cave or the Castle with equal probability and ends with Death (you lose) or Treasure (you win).The outcome depends entirely on luck.The transition probabilities are: Next State Cave Castle Death Treasure Cave .4 .3 .2 .1 Current Castle .5 .3 .1 .1 State Death 0 0 1 0 Treasure 0 0 0 1
A.What is the average number of times you would expect to visit the Cave and the Castle, depending on which state is the starting state?
B.What is the mean time until absorption for the Cave and the Castle?
C.What is the likelihood of winning the game?
(Essay)
4.8/5  (30)
(30)
If all the rows of a transition matrix are identical, there will be no transient states.
(True/False)
4.8/5  (30)
(30)
Retired people often return to the workforce.If a retired woman returns to work at the same place from which she retired -- even if only part time or for a limited term -- that signifies that retirement is not a:
(Multiple Choice)
4.8/5  (45)
(45)
If we perform the calculations for steady-state probabilities for a Markov process with periodic behavior, what do we get?
(Multiple Choice)
4.9/5  (34)
(34)
When calculating steady-state probabilities, we multiply the vector of n unknown values times the transition probability matrix to produce n equations with n unknowns.Why do we arbitrarily drop one of these equations?
(Essay)
4.8/5  (42)
(42)
The transition matrix for customer purchases of alkaline batteries is believed to be as follows: Next Purchase Duracell Eveready Other Current Duracell .43 .35 .22 Purchase Eveready .38 .45 .17 Other .13 .25 .62
A.Based on this transition matrix, what is Duracell's market share for the alkaline battery market?
B.Each 1% of the market share of the alkaline battery market is worth $3.2 million in profit.Suppose that Duracell is contemplating an advertising campaign which it believes will result in the transition probabilities for battery purchases to be as follows:
Next Purchase Duracell Eveready Other Current Duracell .47 .31 .22 Purchase Eveready .38 .40 .22 Other .22 .25 .53
What is the most that Duracell should be willing to pay for this
campaign?
(Essay)
4.7/5  (47)
(47)
A gambler has an opportunity to play a coin tossing game in which he wins his wager with probability .49 and loses his wager with probability .51.Suppose the gambler's initial stake is $40 and the gambler will continue to make $10 bets until his fortune either reaches $0 or $100 (at which time play will stop).Which of the following statements is true?
(Multiple Choice)
4.7/5  (38)
(38)
If we add up the values in the n rows of the fundamental matrix for a Markov process with absorbing states, what is the result?
(Multiple Choice)
4.8/5  (24)
(24)
Consider the transition matrix:
.3 .2 .5 \mid.1 .6 .3\mid \mid.2 .3 .5\mid
The steady-state probability of being in state 1 is approximately:
(Multiple Choice)
4.8/5  (40)
(40)
What is the steady-state significance, if any, of a zero in the transition matrix?
(Essay)
4.8/5  (39)
(39)
Is this an identity matrix? Explain your answer.
| 0 1 0 |
| 1 0 0 |
| 0 0 1 |
(Essay)
4.9/5  (38)
(38)
A Markovian system is currently at stage 1.To determine the state of the system at stage 6, we must have, in addition to the transition matrix, the state probabilities at:
(Multiple Choice)
4.9/5  (36)
(36)
Suppose you play a coin flipping game with a friend in which a fair coin is used.If the coin comes up heads you win $1 from yourfriend, if the coin comes up tails, your friend wins $1 from you.
You have $3 and your friend has $4.You will stop the game when one
of you is broke.Determine the probability that you will win all of your friend's money.
(Short Answer)
4.8/5  (37)
(37)
For Markov processes with absorbing states, steady-state behavior is independent of the initial process state.
(True/False)
4.9/5  (33)
(33)
If a Markov process consists of two absorbing states and two nonabsorbing states, the limiting probabilities for the nonabsorbing states will:
(Multiple Choice)
4.8/5  (30)
(30)
For a Markov process with absorbing states, we define Π(j) = state vector at stage j N = fundamental matrix
I = identity matrix
Q = matrix of transition probabilities between non-absorbing states
R = matrix of transition probabilities between non-absorbing states and absorbing states
The limiting state probabilities equal:
(Multiple Choice)
4.8/5  (40)
(40)
Markovian transition matrices are necessarily square.That is, there are exactly the same number of rows as there are columns.
(True/False)
4.9/5  (38)
(38)
The transition matrix 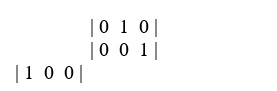 Represents what type of Markov process?
Represents what type of Markov process?
(Multiple Choice)
4.9/5  (33)
(33)
In a Markov process, an absorbing state is a special type of transient state.
(True/False)
4.7/5  (32)
(32)
Showing 21 - 40 of 49
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)