Caspian Seafoods has recently purchased a very large property for possible expansion of its business.On this property, Caspian may construct a large plant (X1) or a small plant (X2).In addition, if, and only if, it constructs either plant, it may or may not choose to build a warehouse (X3) as well.That is, no plant also means no warehouse.Caspian has other expansion opportunities as well, and is using binary (0 - 1) programming for evaluation.Write a linear constraint (or constraints) that adequately and appropriately reflects the stated conditions on X1, X2, and X3 under binary programming.

(Two new linear constraints are required: (1) X 1 + X 2 $\le$ 1 and (2) X 3 - X 1 - X 2 $\le$ 0.The first constraint says that X 1 = 1, X 2 = 1, or both = 0.The second constraint says that if X 1 and X 2 are both 0, then X 3 must also be 0, otherwise X 3 can be 1.That is, if either plant is built, the warehouse can be built.)

Hong Securities has $300,000 to invest in four stocks and three bonds.X1, X2, X3, and X4 denote the amounts invested in each of the stocks, and Y1, Y2, and Y3 equal the amounts invested in each of the three bonds.Which of the following shows that at least 40% of the investment in stocks must be in stock 1?

A) X1 $\ge$ 120,000 B) X1 - .4X2 -.4X3 - .4X4 $\ge$ 0 C) .6X1 - .4X2 - .4X3 - .4X4 $\ge$ 0 D) X1 $\ge$ .4(X2 + X3 + X4 + Y1 + Y2 + Y3) A) X1 $\ge$ 120,000 B) X1 - .4X2 -.4X3 - .4X4 $\ge$ 0 C) .6X1 - .4X2 - .4X3 - .4X4 $\ge$ 0 D) X1 $\ge$ .4(X2 + X3 + X4 + Y1 + Y2 + Y3)

Exam 3: Applications of Linear and Integer Programming Models

It takes two pounds of steel and three pounds of copper to make a particular product.If there are 100 pounds of steel and 100 pounds of cooper available, one constraint will be 2X₁ + 3X₂ $\le$ 200.

Free

(True/False)

4.9/5

(28)

Question 1

Correct Answer:

Verified

False

Appalachian Coal Company must mine a minimum of 30 tons of coal weekly.It can mine at any of four sites.Relevant data concerning fixed weekly operation costs of the sites, variable mining costs per ton of coal, and estimated maximum weekly output of coal at each site are given in the following table.Formulate a mixed integer programming model and solve for the mining strategy that will minimize total weekly costs. Site Weekly Operating Mining Costs Per Maximum Weekly Costs \ 100s Ton \ 100s Output (Tons) \ 5 \ 12 10 \ 6 \ 8 20 \ 2 \ 14 25 \ 7 \ 6 15

Free

(Essay)

4.7/5

(38)

Question 2

Correct Answer:

Verified

(X_j = tons of coal mined at site j.Y_j = 0 or 1 depending on whether or not the site is operational.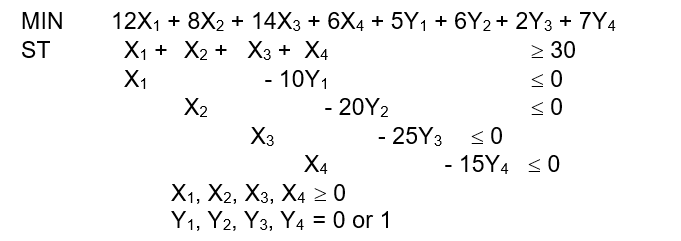

The optimal solution from Excel is to produce 15 tons from site B and 15 tons from site D.Total weekly cost = $223,000.)

Caspian Seafoods has recently purchased a very large property for possible expansion of its business.On this property, Caspian may construct a large plant (X₁) or a small plant (X₂).In addition, if, and only if, it constructs either plant, it may or may not choose to build a warehouse (X₃) as well.That is, no plant also means no warehouse.Caspian has other expansion opportunities as well, and is using binary (0 - 1) programming for evaluation.Write a linear constraint (or constraints) that adequately and appropriately reflects the stated conditions on X₁, X₂, and X₃ under binary programming.

Free

(Essay)

4.8/5

(28)

Question 3

Correct Answer:

Verified

(Two new linear constraints are required: (1) X₁ + X₂ $\le$ 1 and (2) X₃ - X₁ - X₂ $\le$ 0.The first constraint says that X₁ = 1, X₂ = 1, or both = 0.The second constraint says that if X₁ and X₂ are both 0, then X₃ must also be 0, otherwise X₃ can be 1.That is, if either plant is built, the warehouse can be built.)

The optimal solution value of an integer linear programming problem with a minimization objective function may not be __________ the optimal solution value if integer requirements are ignored.

(Multiple Choice)

4.8/5

(38)

Question 4

Nimble Automotive uses linear programming to produce a monthly production schedule for their manufacturing plant.Although the number of cars built is obviously an integer, the fractional part of a non-integer decision variable could be considered "work in progress" at the end of the month.

(True/False)

4.8/5

(38)

Question 5

For the Eastern Engineering problem in question 7, suppose the budget is increased to $600,000 and that the additional engineers or additional staff (but not both) can be hired so that only one of the engineer or staff limitations must hold (i.e.at least one of the two constraints holds).Also, if project 2 is performed, project 5 will not be performed, at least two of projects 1, 2, and 3 should be performed, and if project 3 is performed, project 4 should be performed.Which projects should Eastern undertake under these conditions?

(Essay)

5.0/5

(37)

Question 6

A maximization integer linear model is solved by first relaxing the integer restrictions, giving an optimal solution to the resulting linear model of X₁ = 6, X₂ = 11.The shadow price for the first constraint is $9, and the range of feasibility has a maximum increase of 20 and a maximum decrease of 5.Then for the integer model, X₁ = 6, X₂ = 11 is the optimal solution.If there is an increase of 3 units of the first resource, the optimal value of the objective function will increase by $27.

(True/False)

4.7/5

(34)

Question 7

Nike may build a factory at Millville (Y₁) or it may not.It may also build a regional warehouse at the same site (W₁).But Nike will not build a warehouse without also building a factory.So, its choices are: (1) neither factory nor warehouse; (2) factory only; or (3) factory and warehouse.The appropriate linear constraint to express this is:

(Multiple Choice)

5.0/5

(36)

Question 8

Adding a constraint increases the time needed to solve a linear programming model.Why then might adding a summation variable actually improve model efficiency?

(Essay)

4.7/5

(34)

Question 9

You are currently paying $12 per hour for labor, and labor costs are included in the calculation of the objective function coefficients of a maximization problem.The shadow price for labor printed on the sensitivity analysis report is $8.It would be economically beneficial to you if you could secure extra labor for $15 per hour.

(True/False)

4.8/5

(39)

Question 10

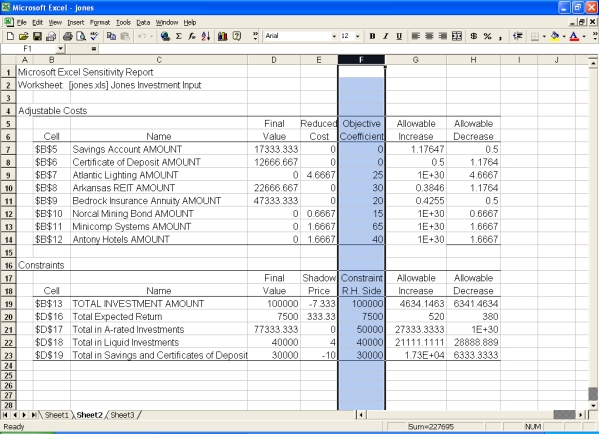Review this Excel spreadsheet: Based on the figures in the spreadsheet, we can conclude:

(Multiple Choice)

4.9/5

(30)

Question 11

Review the Excel spreadsheet below. 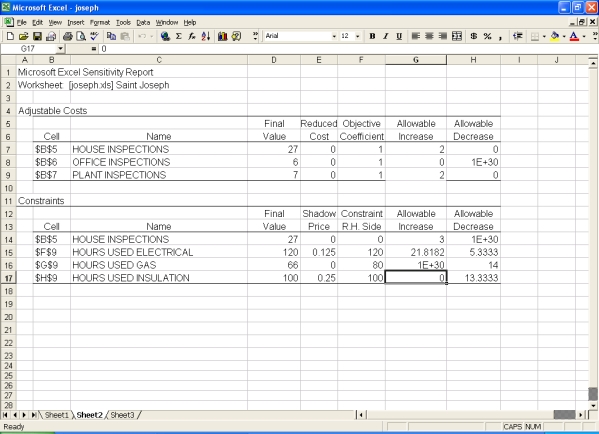Based on the information in the spreadsheet, we can conclude:

(Multiple Choice)

4.9/5

(27)

Question 12

Silver's Gym offers Kickboxing I, Kickboxing II, and Kickboxing III, and Ms.DeVore insists on teaching all three classes.Otherwise, the gym will offer no kickboxing classes.How would you model this constraint?

(Multiple Choice)

4.9/5

(33)

Question 13

Marc Leaser, who has a PhD from MIT, has created a process model using first and second order differential equations.He correctly points out that your linear programming model of the same process makes significant simplifying assumptions which make the linear solution suboptimal.What is your reply to management?

(Essay)

4.8/5

(36)

Question 14

Kings Department Store has 625 rubies, 800 diamonds, and 700 emeralds from which they will make bracelets and necklaces that they have advertised in their Christmas brochure.Each of the rubies is approximately the same size and shape as the diamonds and the emeralds.Kings will net a profit of $250 on each bracelet, which is made with 2 rubies, 3 diamonds, and 4 emeralds, and $500 on each necklace, which includes 5 rubies, 7 diamonds, and 3 emeralds.How many of each should Kings make to maximize its profit?

(Essay)

4.9/5

(32)

Question 15

Hong Securities has $300,000 to invest in four stocks and three bonds.X₁, X₂, X₃, and X₄ denote the amounts invested in each of the stocks, and Y₁, Y₂, and Y₃ equal the amounts invested in each of the three bonds.Which of the following shows that at least 40% of the investment in stocks must be in stock 1?

(Multiple Choice)

4.9/5

(33)

Question 16

Which of the following is true when using summation variables?

(Multiple Choice)

4.9/5

(32)

Question 17

If at most 3 of 7 projects are to be performed, this can be modeled by X₁ + X₂ + X₃ + X₄ + X₅ + X₆ + X₇ $\le$ 3, where X₁, X₂, X₃, X₄, X₅, X₆, and X₇ are all restricted to be non-negative, have an upper bound of 1, and be integer-valued.

(True/False)

4.9/5

(45)

Question 18

The optimal linear programming solution to the Kings Department Store problem in problem 1 is 131.58 bracelets and 57.89 necklaces. A.Characterize the (i) rounded off solution; and (ii) the rounded down solution. B.The shadow price associated with emeralds in the linear programming solution is $13.16, and the upper limit of the range of feasibility for emeralds is 1066.67.A gem buyer at Kings reasoned that since the purchase of emeralds is an included cost, he should be willing to pay up to $13.16 above Kings' current cost for emeralds.When he found a seller who would sell him 100 additional emeralds at $13.00 over the original cost, he purchased them, figuring it would add 100($13.16 - $13.00) = $16 to company profits.He said, "Hey, $16 is $16." Why might he be looking for another job?

(Essay)

4.8/5

(28)

Question 19

Billyboy Toys' toy balls, bats, and gloves net profits, excluding fixed costs, of $7, $8, and $13 respectively.The products require 2, 3, and 5 production hours each.Using current facilities, 1600 production hours are available for the production of these products each month.If Billyboy also leases a second, smaller production facility for $3000 per month, this will increase the availability of production hours for these products by 800.This situation can be modeled using a mixed integer model that includes the following:

(Multiple Choice)

5.0/5

(33)

Question 20

Showing 1 - 20 of 53

It takes two pounds of steel and three pounds of copper to make a particular product.If there are 100 pounds of steel and 100 pounds of cooper available, one constraint will be 2X₁ + 3X₂ $\le$ 200.

The optimal solution value of an integer linear programming problem with a minimization objective function may not be __________ the optimal solution value if integer requirements are ignored.

Nimble Automotive uses linear programming to produce a monthly production schedule for their manufacturing plant.Although the number of cars built is obviously an integer, the fractional part of a non-integer decision variable could be considered "work in progress" at the end of the month.

Adding a constraint increases the time needed to solve a linear programming model.Why then might adding a summation variable actually improve model efficiency?

Review this Excel spreadsheet: Based on the figures in the spreadsheet, we can conclude:

Review the Excel spreadsheet below. Based on the information in the spreadsheet, we can conclude:

Silver's Gym offers Kickboxing I, Kickboxing II, and Kickboxing III, and Ms.DeVore insists on teaching all three classes.Otherwise, the gym will offer no kickboxing classes.How would you model this constraint?

Which of the following is true when using summation variables?

If at most 3 of 7 projects are to be performed, this can be modeled by X₁ + X₂ + X₃ + X₄ + X₅ + X₆ + X₇ $\le$ 3, where X₁, X₂, X₃, X₄, X₅, X₆, and X₇ are all restricted to be non-negative, have an upper bound of 1, and be integer-valued.

Introduction to Management Science Models

Introduction to Management Science Models

Network Models

Project Scheduling Models

Decision Models

Forecasting

Inventory Models

Queuing Models

Simulation Models

Quality Management Models

Markov Process Models

Nonlinear Models:dynamic, Goal, and Nonlinear Programming

Filters

Exam 3: Applications of Linear and Integer Programming Models

It takes two pounds of steel and three pounds of copper to make a particular product.If there are 100 pounds of steel and 100 pounds of cooper available, one constraint will be 2X1 + 3X2 ≤\le≤ 200.

The optimal solution value of an integer linear programming problem with a minimization objective function may not be __________ the optimal solution value if integer requirements are ignored.

Nimble Automotive uses linear programming to produce a monthly production schedule for their manufacturing plant.Although the number of cars built is obviously an integer, the fractional part of a non-integer decision variable could be considered "work in progress" at the end of the month.

Adding a constraint increases the time needed to solve a linear programming model.Why then might adding a summation variable actually improve model efficiency?

Review this Excel spreadsheet: Based on the figures in the spreadsheet, we can conclude:

Review the Excel spreadsheet below. Based on the information in the spreadsheet, we can conclude:

Silver's Gym offers Kickboxing I, Kickboxing II, and Kickboxing III, and Ms.DeVore insists on teaching all three classes.Otherwise, the gym will offer no kickboxing classes.How would you model this constraint?

Which of the following is true when using summation variables?

If at most 3 of 7 projects are to be performed, this can be modeled by X1 + X2 + X3 + X4 + X5 + X6 + X7 ≤\le≤ 3, where X1, X2, X3, X4, X5, X6, and X7 are all restricted to be non-negative, have an upper bound of 1, and be integer-valued.

Introduction to Management Science Models

Introduction to Management Science Models

Network Models

Project Scheduling Models

Decision Models

Forecasting

Inventory Models

Queuing Models

Simulation Models

Quality Management Models

Markov Process Models

Nonlinear Models:dynamic, Goal, and Nonlinear Programming

Filters

It takes two pounds of steel and three pounds of copper to make a particular product.If there are 100 pounds of steel and 100 pounds of cooper available, one constraint will be 2X₁ + 3X₂ $\le$ 200.

If at most 3 of 7 projects are to be performed, this can be modeled by X₁ + X₂ + X₃ + X₄ + X₅ + X₆ + X₇ $\le$ 3, where X₁, X₂, X₃, X₄, X₅, X₆, and X₇ are all restricted to be non-negative, have an upper bound of 1, and be integer-valued.