Exam 7: Systems Of Equations and Inequalities
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
An investor has $450,000 to invest in two types of investments.Type A pays 6% annually and type B pays 7% annually.To have a well-balanced portfolio, the investor imposes the following conditions.At least one-third of the total portfolio is to be allocated to type A investments and at least one-third of the portfolio is to be allocated to type B investments.What is the optimal amount that should be invested in each investment? 
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
E
Write the partial fraction decomposition of the improper rational expression.
Free
(Multiple Choice)
4.7/5  (29)
(29)
Correct Answer:
B
Use any method to solve the system of linear equations, find (x,y).
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
E
Use back-substitution to solve the system of linear equations.
(Multiple Choice)
4.9/5  (39)
(39)
Determine whether the ordered triple is a solution of the system of equations.
(True/False)
5.0/5  (33)
(33)
Use back-substitution to solve the system of linear equations.
(Multiple Choice)
4.8/5  (38)
(38)
For the rational expression the partial fraction decomposition is of the form .
(True/False)
4.7/5  (23)
(23)
Find the equilibrium point (x,p) of the demand and supply equations.(The equilibrium point is the price p and number of units x that satisfy both the demand and supply equations.) Demand Supply p=570-0.5x p=370+0.3x
(Multiple Choice)
4.9/5  (31)
(31)
Find the maximum value of the objective function and where it occurs, subject to the indicated constraints.
Objective function:
Z = 4x + 5y
Constraints:
X ≥ 0
3x - y ≤ 9
2x + 3y ≥ 6
X + 4y ≤ 16
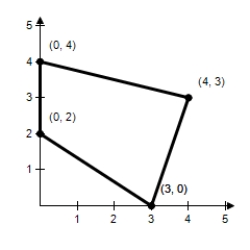
(Multiple Choice)
4.9/5  (34)
(34)
A chemist needs 10 liters of a 25% acid solution.The solution is to be mixed from three solutions whose concentrations are 10%, 20%, and 50%.How many liters of each solution will satisfy each condition? Use 2 liters of the 50% solution.
(Multiple Choice)
4.9/5  (30)
(30)
Use any method to solve the system of linear equations, find (x,y).
(Multiple Choice)
4.9/5  (37)
(37)
Solve the system of linear equations and check any solution algebraically.
(Multiple Choice)
4.8/5  (37)
(37)
Seven hundred gallons of 87-octane gasoline is obtained by mixing 87-octane gasoline with 90-octane gasoline.Use a graphing utility to graph the two given equations.Let x and y represent the number of gallons of the 87-octane gasoline and 90-octane gasoline.As the number of gallons of the 87-octane gasoline increases, how does the number of gallons of the 90-octane gasoline change
(Multiple Choice)
4.8/5  (43)
(43)
Select the region determined by the constraints.Then find the maximum value of the objective function (if possible) and where it occurs, subject to the indicated constraints.
Objective function:
Z = 8x + 9y
Constraints:
X ≥ 0
Y ≥ 0
X + y ≥ 8
3x + 5y ≥ 30
(Multiple Choice)
4.8/5  (44)
(44)
Find the consumer surplus and producer surplus.
Demand
Supply
(Multiple Choice)
4.8/5  (34)
(34)
Write the partial fraction decomposition of the rational expression.Check your result algebraically.
(Multiple Choice)
4.8/5  (31)
(31)
The linear programming problem has an unusual characteristic.Select a graph of the solution region for the problem and describe the unusual characteristic.Find the minimum value of the objective function (if possible) and where it occurs.
Z = x + 3y
Constraints:
X ≥ 0
Y ≥ 0
X + 2y ≤ 4
2x + y ≤ 4
(Multiple Choice)
4.9/5  (33)
(33)
Showing 1 - 20 of 305
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)