Exam 7: Mathematics of Finance
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
Suppose Becky has her choice of $20,000 at the end of each month for life or a single prize of $1.5 million. She is 35 years old and her life expectancy is 40 more years. Find the present value of the annuity if money is worth an annual rate of 7.6%, compounded monthly. Round your answer to the nearest cent.
Free
(Multiple Choice)
4.7/5  (29)
(29)
Correct Answer:
D
State whether the problem relates to an ordinary annuity or an annuity due. A property owner has several rental units and wants to build more. How much of each month's rental income should be deposited at the beginning of each month in an account that earns an annual rate of 6.9%, compounded monthly, if the goal is to have $200,000 at the end of 7 years?
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
B
Find S: 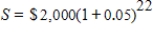 . Round your answer to the nearest cent.
. Round your answer to the nearest cent.
Free
(Multiple Choice)
4.7/5  (35)
(35)
Correct Answer:
C
How much more interest will be earned if $7,500 is invested for 7 years at an annual rate of 12% compounded continuously, instead of at 12% compounded quarterly? Round your answer to the nearest cent.
(Multiple Choice)
4.7/5  (39)
(39)
A small business owner contributes $2,000 at the end of each quarter to a retirement account that earns an annual rate of 6.5% compounded quarterly. How long will it be until the account is worth $250,000? Round your answer to the nearest whole number.
(Multiple Choice)
4.9/5  (39)
(39)
Suppose you are offered a job paying a starting salary of $18,000 with yearly raises of $900. How much will you receive for your 18th year on the job?
(Multiple Choice)
4.8/5  (39)
(39)
If $5,000 is deposited at the end of each half year in an account that earns an annual rate of 6.0% compounded semiannually, how long will it be before the account contains $145,000? Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (31)
(31)
$3,300 is invested for 8 months at an annual simple interest rate of 21%. How much interest will be earned? Round your answer to the nearest dollar.
(Multiple Choice)
4.9/5  (30)
(30)
Suppose a new business makes a $1,000 profit in its first month and has its profit increase by 9% each month for the next 2 years. How much profit will it earn in its first year? Round your answer to the nearest cent.
(Multiple Choice)
5.0/5  (34)
(34)
A young couple buying their first home borrows $72,000 for 28 years at 8.8%, compounded monthly, and makes payments of $577.59. After 2 years, they are able to make a one-time payment of $5,000 along with their 24th payment. How much will the couple save over the life of the loan by paying the extra $5,000? Round your answer to the nearest dollar.
(Multiple Choice)
4.8/5  (24)
(24)
What are d and a1 in the following arithmetic sequence?
2, 3, 4,...
(Multiple Choice)
4.8/5  (31)
(31)
Suppose that Craig Nordstrom deposits his $11,500 bonus in an account that earns an annual rate of 7.5%, compounded quarterly, and makes additional deposits of $800 at the end of each quarter for the next 24.5 years, until he retires. How much is in the account after the last deposit is made? Round your answer to the nearest cent.
(Multiple Choice)
4.8/5  (36)
(36)
Suppose an annuity will pay $12,000 at the beginning of each year for the next 10 years. How much money is needed to start this annuity if it earns 6.7%, compounded annually? Round your answer to the nearest cent.
(Multiple Choice)
4.9/5  (41)
(41)
A woman buys an apartment house for $1,250,000 by making a down payment of $325,000 and amortizing the rest of the debt with semiannual payments over the next 11 years. The annual interest rate on the debt is 8%, compounded semiannually. Find the size of each payment. Round your answer to the nearest cent.
(Multiple Choice)
4.8/5  (34)
(34)
A year-end bonus of $15,000 will generate how much money at the beginning of each month for the next year, if it can be invested at 6.48%, compounded monthly? Round your answer to the nearest cent.
(Multiple Choice)
4.9/5  (34)
(34)
Find the present value of an annuity of $1,800, at the end of each quarter for 8 years after being deferred for 6 years, if the money is worth an annual rate of 8.8% compounded quarterly. Round your answer to the nearest cent.
(Multiple Choice)
4.8/5  (31)
(31)
Find the 35th term of the arithmetic sequence with first term 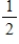 and common difference
and common difference 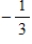 .
.
(Multiple Choice)
4.9/5  (37)
(37)
State whether the problem relates to an ordinary annuity or an annuity due. Mr. Gordon plans to invest $500 at the end of each month in an account that pays an annual rate of 9%, compounded monthly. After how many months will the account be worth $60,000?
(Multiple Choice)
4.8/5  (30)
(30)
A young executive deposits $300 at the end of each month for 6 years and then increases the deposits. If the account earns an annual rate of 8.3%, compounded monthly, how much (to the nearest dollar) should each new deposit be in order to have a total of $400,000 after 21 years from the time the deposits were increased? Round your answer to the nearest dollar.
(Multiple Choice)
4.9/5  (32)
(32)
During four years of college, Nolan MacGregor's student loans are $3,600, $3,900, $3,500, and $3,600 for freshman year through senior year, respectively. Each loan amount gathers interest of annual rate 1% compounded quarterly while Nolan is in school; and annual rate of 3%, compounded quarterly during a 6-month grace period after graduation. Assume the freshman year loan earns an annual rate of 1% interest for 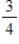 year during the first year, then for 3 full years until graduation. Make similar assumptions for the loans for the other years. After the grace period, the loan is amortized over the next 10 years at an annual rate of 3%, compounded quarterly. If Nolan decides to pay an additional $90 above the calculated quarterly payment, how many payments of this size will amortize the debt? Round your answer to the nearest whole number.
year during the first year, then for 3 full years until graduation. Make similar assumptions for the loans for the other years. After the grace period, the loan is amortized over the next 10 years at an annual rate of 3%, compounded quarterly. If Nolan decides to pay an additional $90 above the calculated quarterly payment, how many payments of this size will amortize the debt? Round your answer to the nearest whole number.
(Multiple Choice)
4.8/5  (24)
(24)
Showing 1 - 20 of 131
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)