Exam 14: Definite Integrals: Techniques of Integration
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
Suppose that the Carter Car Service franchise finds that the income generated by its stores can be modeled by assuming that the income is a continuous stream with a monthly rate of flow at time t given by 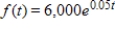 (dollars per month). Find the total income from a Carter Car Service store for years 3 through 5 of operation and round to the nearest penny.
(dollars per month). Find the total income from a Carter Car Service store for years 3 through 5 of operation and round to the nearest penny.
Free
(Multiple Choice)
4.8/5  (44)
(44)
Correct Answer:
D
Use the Trapezoidal Rule to approximate 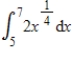 with n = 6. Round your answer to two decimal places.
with n = 6. Round your answer to two decimal places.
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
E
Use the function 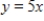 from x = 0 to x = 1 and n equal subintervals with the function evaluated at the left-hand endpoints of each subinterval. Find a formula for the sum of the areas of the n rectangles (call this S).
from x = 0 to x = 1 and n equal subintervals with the function evaluated at the left-hand endpoints of each subinterval. Find a formula for the sum of the areas of the n rectangles (call this S).
(Multiple Choice)
4.9/5  (35)
(35)
Find the producer's surplus for a product if its demand function is 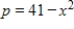 and its supply function is
and its supply function is 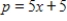 where p is in millions of dollars and x is the number of thousands of units. Round your answer to the nearest million dollars.
where p is in millions of dollars and x is the number of thousands of units. Round your answer to the nearest million dollars.
(Multiple Choice)
4.9/5  (35)
(35)
Use Simpson's Rule to approximate 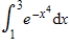 with n = 4. Round your answer to 3 decimal places.
with n = 4. Round your answer to 3 decimal places.
(Multiple Choice)
4.9/5  (36)
(36)
Assume that a store finds that its sales revenue changes at a rate given by 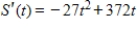 dollars per day, where t is the number of days after an advertising campaign ends and
dollars per day, where t is the number of days after an advertising campaign ends and 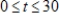 . Find the total sales for the second week after the campaign ends
. Find the total sales for the second week after the campaign ends 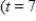 to
to 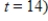 .
.
(Multiple Choice)
4.9/5  (41)
(41)
Find the area of the region enclosed by the graphs of 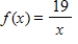 and
and 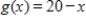 .
.
(Multiple Choice)
4.8/5  (30)
(30)
The following table shows the rate of oil consumption (in thousands of barrels per year) by a certain city. Estimate the total consumption of oil by the city from 1999 -2004 by using 5 equal subdivisions and left-hand endpoints to estimate the area under the graph that corresponds to the table from 1999 to 2004. 
(Multiple Choice)
4.7/5  (35)
(35)
A franchise models the profit from its store as a continuous income stream with a monthly rate of flow at time t given by 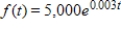 (dollars per month). When a new store opens, its manager is judged against the model, with special emphasis on the second half of the first year. Find the total profit for the second 6-month period
(dollars per month). When a new store opens, its manager is judged against the model, with special emphasis on the second half of the first year. Find the total profit for the second 6-month period 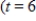 to
to 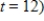 . Round your answer to the nearest dollar.
. Round your answer to the nearest dollar.
(Multiple Choice)
4.7/5  (37)
(37)
Find the value of the given sum and round to four decimal places. 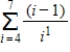
(Multiple Choice)
4.8/5  (32)
(32)
Suppose that a printing firm considers the production of its presses as a continuous income stream. If the annual rate of flow at time t is given by 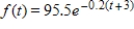 in thousands of dollars per year, and if money is worth 7% compounded continuously, find the present value and future value of the presses over the next 10 years. Round your answer to the nearest dollar.
in thousands of dollars per year, and if money is worth 7% compounded continuously, find the present value and future value of the presses over the next 10 years. Round your answer to the nearest dollar.
(Multiple Choice)
4.8/5  (40)
(40)
Use integration by parts to evaluate 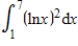 . Note that evaluation may require integration by parts more than once.
. Note that evaluation may require integration by parts more than once.
(Multiple Choice)
4.9/5  (37)
(37)
Suppose the number of daily sales of a product was found to be given by 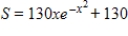 , x days after the start of an advertising campaign for this product. Find the average daily sales during the first 25 days of the campaign-that is, from
, x days after the start of an advertising campaign for this product. Find the average daily sales during the first 25 days of the campaign-that is, from 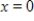 to
to 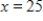 . Round your answer to the nearest dollar.
. Round your answer to the nearest dollar.
(Multiple Choice)
4.9/5  (36)
(36)
The rate of depreciation of a building is given by 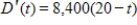 dollars per year,
dollars per year, 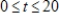 . Use the definite integral to find the total depreciation over the first 20 years.
. Use the definite integral to find the total depreciation over the first 20 years.
(Multiple Choice)
4.9/5  (31)
(31)
Showing 1 - 20 of 185
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)