Exam 5: Inequalities and Linear Programming
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
The simplex matrix shown below indicates that an optimal solution has been found ( 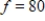 when
when 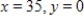 ) but that a second solution is possible. Find the second solution.
) but that a second solution is possible. Find the second solution. 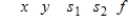

Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
E
Two factories produce three different types of kitchen appliances. The following table summarizes the production capacities, the numbers of each type of appliance ordered, and the daily operating costs for the factories. How many days should each factory operate to fill the orders at minimum cost? Find the minimum cost. 
Free
(Multiple Choice)
4.7/5  (33)
(33)
Correct Answer:
B
The Wellbuilt Company produces two types of wood chippers, economy and deluxe. The deluxe model requires 4 hours to assemble and 0.5 hour to paint, and the economy model requires 2 hours to assemble and 1 hour to paint. The maximum number of assembly hours available is 22 per day, and the maximum number of painting hours available is 8 per day. Let x represent the number of deluxe models and y represent the number of economy models. Write the system of inequalities that describes the constraints on the number of each type of wood chipper produced.
Free
(Multiple Choice)
4.8/5  (29)
(29)
Correct Answer:
C
Nekita Corporation assembles cell phones and camera cell phones at two different factories within the same city. During each hour at the first factory, 15 cell phones and 30 camera cell phones can be assembled at a cost of $130/hour. During each hour at the second factory, 10 cell phones and 60 camera cell phones can be assembled at a cost of $160/hour. If Nekita expects weekly orders for at least 15,000 cell phones and at least 45,000 camera cell phones, how many hours per week should it schedule at each location to be able to fill the orders at minimum cost? What is the minimum cost?
(Multiple Choice)
4.9/5  (37)
(37)
Suppose that an experiment that involves learning in animals requires placing white mice and rabbits into separate, controlled environments, environment I and environment II. The maximum amount of time available in environment I is 300 minutes, and the maximum amount of time available in environment II is 400 minutes. The white mice must spend 20 minutes in environment I and 35 minutes in environment II, and the rabbits must spend 45 minutes in environment I and 50 minutes in environment II. Let x represent number of white mice and y represent number of rabbits. Determine the system of inequalities that describes the constraints on the number of each type of animal used in the experiment. Then graph the solution of the system of inequalities.
(Multiple Choice)
4.7/5  (29)
(29)
Use the simplex method, Excel, or another technology to solve. 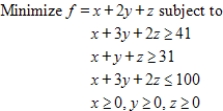
(Multiple Choice)
4.8/5  (33)
(33)
Solve the following linear programming problem.
Maximize 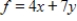 subject to
subject to
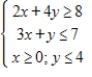
(Multiple Choice)
4.9/5  (32)
(32)
The graph of the boundary equations for the system of inequalities is shown with that system. Locate the solution region and find the corners. 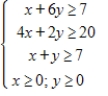
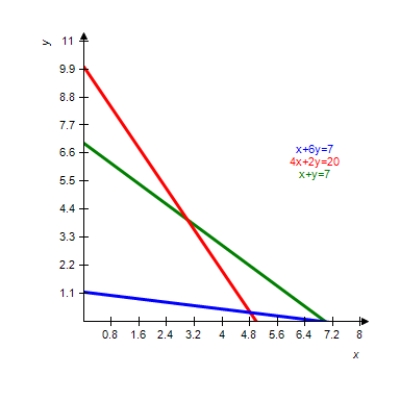
(Multiple Choice)
4.8/5  (31)
(31)
State the given problem in a form from which the simplex matrix can be formed (that is, as a maximization problem with 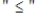 constraints).
Minimize
constraints).
Minimize 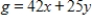 subject to
subject to 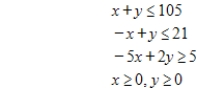
(Multiple Choice)
4.9/5  (38)
(38)
A woman has a building with 26 one-bedroom apartments, 40 two-bedroom apartments, and 60 three-bedroom apartments available to rent to students. She has set the rent at $550 per month for the one-bedroom units, $900 per month for the two-bedroom units, and $1,100 per month for the three-bedroom units. She must rent to one student per bedroom, and zoning laws limit her to at most 250 students in this building. There are enough students available to rent all the apartments. How many of each type of apartment should she rent to maximize her monthly revenue? Find the maximum possible monthly revenue. Round your profit to the nearest dollar.
(Multiple Choice)
4.9/5  (40)
(40)
A pork producer is considering two types of feed that contain the necessary ingredients for the nutritional requirements for fattening hogs. Brand X contains 2 units of ingredient A per pound and 15 units of ingredient B per pound, Brand Y contains 15 units of ingredient A per pound and 2 units of ingredient B per pound. The nutritional requirements for the hogs are at least 120 units of ingredient A and at least 237 units of ingredient B. If brand X costs 65 cents per pound and brand Y costs 80 cents per pound, how many pounds of each brand should be bought to satisfy the nutritional requirements at minimum cost?
(Multiple Choice)
4.8/5  (38)
(38)
A simplex matrix for a standard maximization problem is given. Indicate whether or not the solution shown is complete (optimal). If the solution is not complete, find the next pivot or indicate that no solution exists. 
(Multiple Choice)
4.9/5  (48)
(48)
The graph of the boundary equations for the system of inequalities is shown with that system. Locate the solution region and find the corners. 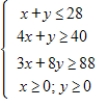
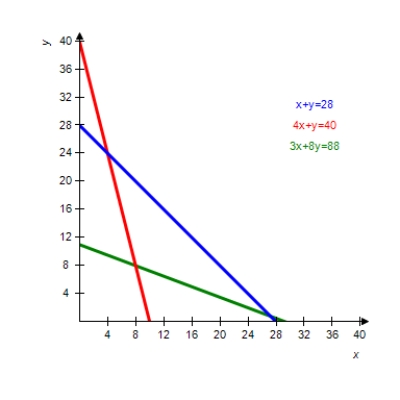
(Multiple Choice)
4.9/5  (45)
(45)
In a laboratory experiment, two separate foods are given to experimental animals. Each food contains essential ingredients, A and B, for which the animals have a minimum requirement, and each food also has an ingredient C, which can be harmful to the animals. The table below summarizes this information. 
How many grams of foods 1 and 2 will satisfy the requirements for A and B and minimize the amount of ingredient C that is ingested? Also what is the minimum amount of ingredient C ingested?
How many grams of foods 1 and 2 will satisfy the requirements for A and B and minimize the amount of ingredient C that is ingested? Also what is the minimum amount of ingredient C ingested?
(Multiple Choice)
5.0/5  (33)
(33)
A farm co-op has over 6,000 acres available to plant with corn and soybeans. The farm co-op's maximum profit for planting 6,000 acres is $315,000 and the maximum profit for 6,008 acres is $315,320. What is the profit value of each additional acre of land? This value is called the shadow price of an acre of land. Round your answer to the nearest cent if necessary.
(Multiple Choice)
4.9/5  (35)
(35)
The James MacGregor Mining Company owns three mines: I, II, and III. Three grades of ore, A, B, and C, are mined at these mines. For each grade of ore, the number of tons per week available from each mine and the number of tons per week required to fill orders are given in the following table. 

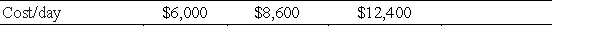
Find the number of days that the company should operate each mine so that orders are filled at minimum cost. Find the minimum cost.
Find the number of days that the company should operate each mine so that orders are filled at minimum cost. Find the minimum cost.
(Multiple Choice)
4.7/5  (36)
(36)
Johnson City Cooperage manufactures 30-gallon and 55-gallon fiber drums. Each 30-gallon drum takes 30 minutes to make, each 55-gallon drum takes 40 minutes to make, and the company has at most 10,000 minutes available each week. Also, workplace limitations and product demand indicate that the number of 55-gallon drums produced plus half the number of 30-gallon drums produced should be at least 160, and the number of 30-gallon drums should be at least twice the number of 55-gallon drums. If Johnson City Cooperage's manufacturing costs are $4.4 for each 30-gallon drum and $6.9 for each 55-gallon drum, how many of each drum should be made each week to satisfy the constraints at minimum cost? Find the minimum cost.
(Multiple Choice)
4.7/5  (35)
(35)
Suppose a primal minimization problem and its dual maximization problem were solved by using the simplex method on the dual problem. The final simplex matrix is given. Find the solution of the maximization problem. Use x1, x2, x3 as the variables and f as the function. 
(Multiple Choice)
4.8/5  (29)
(29)
The Video Star Company makes two different models of DVD players, which are assembled on two different assembly lines. Line 1 can assemble 30 units of the Star model and 42 units of the Prostar model per hour, and Line 2 can assemble 150 units of the Star model and 40 units of the Prostar model per hour. The company needs to produce at least 250 units of the Star model and 210 units of the Prostar model to fill an order. Let x represent the number of assembly hours for Line 1 and y represent the number of assembly hours for Line 2. Graph the region determined by the constraint inequalities.
(Multiple Choice)
4.7/5  (35)
(35)
Showing 1 - 20 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)