Exam 16: Integrating Functions of Several Variables
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Evaluate the integral .Give your answer to two decimal places.
(Short Answer)
4.8/5  (26)
(26)
Let x and y have joint density function Find the probability that x > y +0.4.
(Short Answer)
4.8/5  (44)
(44)
Set up (but do not evaluate)an iterated integral to compute the mass of the solid paraboloid bounded by and z = 1, if the density is given by (x, y, z)= z2.
(Multiple Choice)
4.9/5  (39)
(39)
A solid is bounded below by the triangle z = 0, x 0, y 0, x + y 1 and above by the plane z = x + 6y + 2.If the density of the solid is given by (x, y, z)= z, find its mass.
(Essay)
4.8/5  (35)
(35)
Set up the three-dimensional integral where R is the "ice-cream cone" enclosed by a sphere of radius 2 centered at the origin and the cone .Use rectangular coordinates. 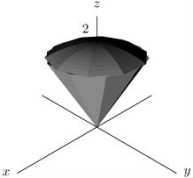
(Multiple Choice)
4.7/5  (42)
(42)
Let R be the region bounded between the two ellipses and Use this change of coordinates for to evaluate the integral
(Multiple Choice)
4.8/5  (40)
(40)
Compute the area of the flower-like region bounded by r = 6 + 3 cos (8 ).
(Essay)
4.8/5  (41)
(41)
The joint density function for random variables x and y is Find the probability .Give your answer to 3 decimal places.
(Short Answer)
4.8/5  (30)
(30)
Upper and lower sums for a function f on a rectangle R, using n subdivisions on each side, are and respectively.Evaluate
(Short Answer)
4.8/5  (41)
(41)
Let f(x, y)be a positive function of x and y which is independent of x, that is, f(x, y)= g(y)for some one-variable function g.Suppose that and .
Find , where R is the rectangle 0 x 3, 0 y 10.
(Short Answer)
4.9/5  (40)
(40)
Consider the volume between a cone centered along the positive z-axis, with vertex at the origin and containing the point (0, 1, 1), and a sphere of radius 3 centered at the origin.
Write a triple integral which represents this volume and evaluate it.Use spherical coordinates.
(Essay)
4.8/5  (34)
(34)
The function has an average value of 4 on the triangle with vertices at (0, 0), (0, 1)and (1, 0).Find the constant a.
(Short Answer)
4.8/5  (31)
(31)
The function has an average value of 16 on the rectangle with vertices at (0, 0),(0, 2), (2, 0)and (2, 2).Find the constant k.
(Short Answer)
4.8/5  (34)
(34)
Showing 61 - 76 of 76
Filters
- Essay(39)
- Multiple Choice(17)
- Short Answer(18)
- True False(2)
- Matching(0)