Exam 4: Exponential and Logarithmic Functions
Exam 1: Equations and Inequalities419 Questions
Exam 2: Functions and Graphs144 Questions
Exam 3: Polynomial and Rational Functions224 Questions
Exam 4: Exponential and Logarithmic Functions146 Questions
Exam 5: Systems of Equations and Inequalities160 Questions
Select questions type
Solve the problem.
-A city is growing at the rate of annually. If there were residents in the city in 1994 , find how many (to the nearest ten-thousand) are living in that city in 2000 . Use .
(Multiple Choice)
4.7/5  (30)
(30)
Graph the function.
-Use the graph of to obtain the graph of .
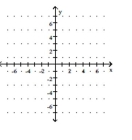
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-The rabbit population in a forest area grows at the rate of monthly. If there are 150 rabbits in September, find how many rabbits (rounded to the nearest whole number) should be expected by next September. Use .
(Multiple Choice)
4.9/5  (35)
(35)
Evaluate or simplify the expression without using a calculator.
-
(Multiple Choice)
4.9/5  (45)
(45)
Evaluate or simplify the expression without using a calculator.
-
(Multiple Choice)
4.9/5  (33)
(33)
Graph the function.
-Use the graph of to obtain the graph of .
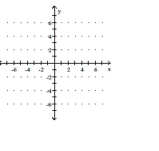
(Multiple Choice)
4.9/5  (34)
(34)
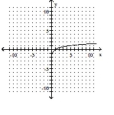
The graph of a logarithmic function is given. Select the function for the graph from the options.
-
(Multiple Choice)
4.8/5  (31)
(31)
Evaluate or simplify the expression without using a calculator.
-
(Multiple Choice)
4.9/5  (41)
(41)
Graph the function.
-Use the graph of to obtain the graph of
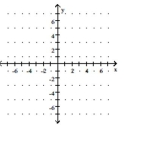
(Multiple Choice)
4.9/5  (35)
(35)
-Find the accumulated value of an investment of $940 at 6% compounded annually for 6 years.
(Multiple Choice)
4.9/5  (40)
(40)
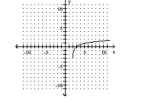
The graph of a logarithmic function is given. Select the function for the graph from the options.
-
(Multiple Choice)
4.9/5  (41)
(41)
Solve the problem.
-The function models the amount in pounds of a particular radioactive material stored in a concrete vault, where is the number of years since the material was put into the vault. Find the amount of radioactive material in the vault after 140 years. Round to the nearest whole number.
(Multiple Choice)
4.7/5  (36)
(36)
Approximate the number using a calculator. Round your answer to three decimal places.
-
(Multiple Choice)
4.9/5  (39)
(39)
Graph the function.
-Use the graph of to obtain the graph of .
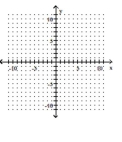
(Multiple Choice)
4.8/5  (31)
(31)
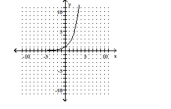
The graph of an exponential function is given. Select the function for the graph from the functions listed.
-
(Multiple Choice)
4.8/5  (35)
(35)
Graph the function.
-Use the graph of to obtain the graph of
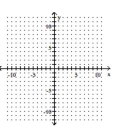
(Multiple Choice)
4.8/5  (46)
(46)
Evaluate or simplify the expression without using a calculator.
-
(Multiple Choice)
4.9/5  (27)
(27)
Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate
logarithmic expressions without using a calculator.
-
(Multiple Choice)
4.8/5  (26)
(26)
Graph the function.
-Use the graph of to obtain the graph of
(Multiple Choice)
4.7/5  (34)
(34)
Showing 101 - 120 of 146
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)