Question 1

Write the equation in its equivalent logarithmic form.
-$b ^ { 3 } = 2744$

Accepted Answer

A)  $\log _ { b } 3 = 2744$ 
B)  $\log _ { 3 } 2744 = \mathrm { b }$ 
C)  $\log _ { b } 2744 = 3$ 
D)  $\log 2744 \mathrm {~b} = 3$ 
A)  $\log _ { b } 3 = 2744$ 
B)  $\log _ { 3 } 2744 = \mathrm { b }$ 
C)  $\log _ { b } 2744 = 3$ 
D)  $\log 2744 \mathrm {~b} = 3$

Question 2

Find the domain of the logarithmic function.
-$$f ( x ) = \log _ { 5 } ( x - 2 ) ^ { 2 }$$

Accepted Answer

A)  $( - \infty , 0 )$ or $( 0 , \infty )$ 
B)  $( - \infty , 2 )$ or $( 2 , \infty )$ 
C)  $( - 2 , \infty )$ 
D)  $( 2 , \infty )$ 
A)  $( - \infty , 0 )$ or $( 0 , \infty )$ 
B)  $( - \infty , 2 )$ or $( 2 , \infty )$ 
C)  $( - 2 , \infty )$ 
D)  $( 2 , \infty )$

Question 3

The graph of a logarithmic function is given. Select the function for the graph from the options.
-

Accepted Answer

A)  $f ( x ) = 1 - \log _ { 5 } x$ 
B)  $f ( x ) = \log _ { 5 } x$ 
C)  $f ( x ) = - \log _ { 5 } x$ 
D)  $f ( x ) = \log _ { 5 } ( - x )$ 
A)  $f ( x ) = 1 - \log _ { 5 } x$ 
B)  $f ( x ) = \log _ { 5 } x$ 
C)  $f ( x ) = - \log _ { 5 } x$ 
D)  $f ( x ) = \log _ { 5 } ( - x )$

Question 4

Evaluate the expression without using a calculator.
-$\log _ { 27 } 3$

Accepted Answer

A)  9 
B)  1 
C)  3 
D)  $\frac { 1 } { 3 }$ 
A)  9 
B)  1 
C)  3 
D)  $\frac { 1 } { 3 }$

Question 5

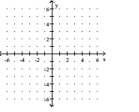
Graph the function.
-Use the graph of $f ( x ) = 4 ^ { x }$ to obtain the graph of $g ( x ) = 4 ^ { - x }$.

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 6

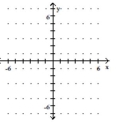
Graph the functions in the same rectangular coordinate system.
-$f(x)=3^{x} \text { and } g(x)=\log _{3} x$

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 7

Graph the function.
-Use the graph of $\log _ { 5 } x$ to obtain the graph of $f ( x ) = \frac { 1 } { 2 } \log _ { 5 } x$.

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 8

Write the equation in its equivalent logarithmic form.
-$5 ^ { 3 } = x$

Accepted Answer

A)  $\log _ { 3 } x = 5$ 
B)  $\log _ { x } 5 = 3$ 
C)  $\log _ { 5 } 3 = x$ 
D)  $\log _ { 5 } x = 3$ 
A)  $\log _ { 3 } x = 5$ 
B)  $\log _ { x } 5 = 3$ 
C)  $\log _ { 5 } 3 = x$ 
D)  $\log _ { 5 } x = 3$

Question 9

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate
logarithmic expressions without using a calculator.
-$\ln \left( \frac { e ^ { 2 } } { 9 } \right)$

Accepted Answer

A)  $\ln e ^ { 2 } + \ln 9$ 
B)  $\ln e ^ { 2 } - \ln 9$ 
C)  $2 - \ln 9$ 
D)  $2 + \ln 9$ 
A)  $\ln e ^ { 2 } + \ln 9$ 
B)  $\ln e ^ { 2 } - \ln 9$ 
C)  $2 - \ln 9$ 
D)  $2 + \ln 9$

Question 10

Approximate the number using a calculator. Round your answer to three decimal places.
-$2^{ \sqrt { 7 }}$

Accepted Answer

A)  $64.000$ 
B)  $6.258$ 
C)  $5.292$ 
D)  $7.000$ 
A)  $64.000$ 
B)  $6.258$ 
C)  $5.292$ 
D)  $7.000$

Question 11

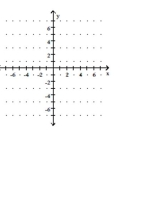
Graph the function.
-Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = e ^ { x / 4 } + 3$.

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 12

Solve the problem.
-The population in a particular country is growing at the rate of $2.8 \%$ per year. If $7,638,000$ people lived there in 1999 , how many will there be in the year 2005 ? Use $\mathrm { f } ( \mathrm { x } ) = \mathrm { y } _ { 0 } \mathrm { e } ^ { 0.028 \mathrm { t } }$ and round to the nearest ten-thousand.

Accepted Answer

A)  $8,850,000$ 
B)  $10,840,000$ 
C)  $9,940,000$ 
D)  $9,040,000$ 
A)  $8,850,000$ 
B)  $10,840,000$ 
C)  $9,940,000$ 
D)  $9,040,000$

Question 13

Solve the problem.
-The long jump record, in feet, at a particular school can be modeled by f(x)= 20.1 + 2.5 ln (x + 1)where x is the number of years since records began to be kept at the school. What is the record for the long jump 6 years after Record started being kept? Round your answer to the nearest tenth.

Accepted Answer

A) 25.0 feet 
B) 22.6 feet 
C) 24.6 feet 
D) 24.1 feet 
A) 25.0 feet 
B) 22.6 feet 
C) 24.6 feet 
D) 24.1 feet

Question 14

Graph the function by making a table of coordinates
-$$f ( x ) = 4 ^ { x }$$

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 15

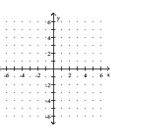
Graph the function.
-Use the graph of $f ( x ) = 2 ^ { x }$ to obtain the graph of $g ( x ) = 2 ^ { x - 3 }$

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 16

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate
logarithmic expressions without using a calculator.
-$\log _ { 5 } \left( \frac { 125 } { \sqrt { x - 1 } } \right)$

Accepted Answer

A)  $3 \log _ { 5 } 5 - \frac { 1 } { 2 } \log _ { 5 } ( x - 1 )$ 
B)  $3 - \log _ { 5 } \sqrt { x - 1 }$ 
C)  $3 - \frac { 1 } { 2 } \log _ { 5 } ( x - 1 )$ 
D)  $\log _ { 5 } 125 - \log _ { 5 } \sqrt { x - 1 }$ 
A)  $3 \log _ { 5 } 5 - \frac { 1 } { 2 } \log _ { 5 } ( x - 1 )$ 
B)  $3 - \log _ { 5 } \sqrt { x - 1 }$ 
C)  $3 - \frac { 1 } { 2 } \log _ { 5 } ( x - 1 )$ 
D)  $\log _ { 5 } 125 - \log _ { 5 } \sqrt { x - 1 }$

Question 17

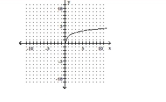
The graph of a logarithmic function is given. Select the function for the graph from the options.
-

Accepted Answer

A)  $f ( x ) = \log _ { 3 } x + 2$ 
B)  $f ( x ) = \log _ { 3 } ( x - 2 )$ 
C)  $f ( x ) = \log _ { 3 } x$ 
D)  $f ( x ) = \log _ { 3 } ( x + 2 )$ 
A)  $f ( x ) = \log _ { 3 } x + 2$ 
B)  $f ( x ) = \log _ { 3 } ( x - 2 )$ 
C)  $f ( x ) = \log _ { 3 } x$ 
D)  $f ( x ) = \log _ { 3 } ( x + 2 )$

Question 18

Solve the problem.
-A sample of $900 \mathrm {~g}$ of lead-210 decays to polonium-210 according to the function given by $\mathrm { A } ( \mathrm { t } ) = 900 \mathrm { e } ^ { - 0.032 \mathrm { t } }$, where $t$ is time in years. What is the amount of the sample after 50 years (to the nearest g)?

Accepted Answer

A)  $182 \mathrm {~g}$ 
B)  $132 \mathrm {~g}$ 
C)  $4458 \mathrm {~g}$ 
D)  $28 \mathrm {~g}$ 
A)  $182 \mathrm {~g}$ 
B)  $132 \mathrm {~g}$ 
C)  $4458 \mathrm {~g}$ 
D)  $28 \mathrm {~g}$

Question 19

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate
logarithmic expressions without using a calculator.
-$\ln \sqrt [ 3 ] { \mathrm { ey } }$

Accepted Answer

A)  $\frac { y } { 3 }$ 
B)  $\frac { 1 } { 3 } \ln \sqrt [ 3 ] { \mathrm { ey } } + \frac { 1 } { 3 }$ 
C)  $3 \ln y + 3$ 
D)  $\frac { 1 } { 3 } \ln y + \frac { 1 } { 3 }$ 
A)  $\frac { y } { 3 }$ 
B)  $\frac { 1 } { 3 } \ln \sqrt [ 3 ] { \mathrm { ey } } + \frac { 1 } { 3 }$ 
C)  $3 \ln y + 3$ 
D)  $\frac { 1 } { 3 } \ln y + \frac { 1 } { 3 }$

Question 20

Evaluate the expression without using a calculator.
-$\log _ { 2 } \frac { 1 } { 4 }$

Accepted Answer

A)  $- 2$ 
B)  4 
C)  2 
D)  $\frac { 1 } { 2 }$ 
A)  $- 2$ 
B)  4 
C)  2 
D)  $\frac { 1 } { 2 }$

Write the equation in its equivalent logarithmic form. - $b ^ { 3 } = 2744$

Find the domain of the logarithmic function. - $f ( x ) = \log _ { 5 } ( x - 2 ) ^ { 2 }$

The graph of a logarithmic function is given. Select the function for the graph from the options. -

Evaluate the expression without using a calculator. - $\log _ { 27 } 3$

Graph the function. -Use the graph of $f ( x ) = 4 ^ { x }$ to obtain the graph of $g ( x ) = 4 ^ { - x }$ . $Graph the function. -Use the graph of f ( x ) = 4 ^ { x } to obtain the graph of g ( x ) = 4 ^ { - x } .$

Graph the functions in the same rectangular coordinate system. - $f(x)=3^{x} \text { and } g(x)=\log _{3} x$ $Graph the functions in the same rectangular coordinate system. - f(x)=3^{x} \text { and } g(x)=\log _{3} x$

Graph the function. -Use the graph of $\log _ { 5 } x$ to obtain the graph of $f ( x ) = \frac { 1 } { 2 } \log _ { 5 } x$ . $Graph the function. -Use the graph of \log _ { 5 } x to obtain the graph of f ( x ) = \frac { 1 } { 2 } \log _ { 5 } x .$

Write the equation in its equivalent logarithmic form. - $5 ^ { 3 } = x$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\ln \left( \frac { e ^ { 2 } } { 9 } \right)$

Approximate the number using a calculator. Round your answer to three decimal places. - $2^{ \sqrt { 7 }}$

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = e ^ { x / 4 } + 3$ . $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = e ^ { x / 4 } + 3 .$

Graph the function by making a table of coordinates - $f ( x ) = 4 ^ { x }$ $Graph the function by making a table of coordinates - f ( x ) = 4 ^ { x }$

Graph the function. -Use the graph of $f ( x ) = 2 ^ { x }$ to obtain the graph of $g ( x ) = 2 ^ { x - 3 }$ $Graph the function. -Use the graph of f ( x ) = 2 ^ { x } to obtain the graph of g ( x ) = 2 ^ { x - 3 }$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log _ { 5 } \left( \frac { 125 } { \sqrt { x - 1 } } \right)$

The graph of a logarithmic function is given. Select the function for the graph from the options. -

Solve the problem. -A sample of $900 \mathrm {~g}$ of lead-210 decays to polonium-210 according to the function given by $\mathrm { A } ( \mathrm { t } ) = 900 \mathrm { e } ^ { - 0.032 \mathrm { t } }$ , where $t$ is time in years. What is the amount of the sample after 50 years (to the nearest g)?

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\ln \sqrt [ 3 ] { \mathrm { ey } }$

Evaluate the expression without using a calculator. - $\log _ { 2 } \frac { 1 } { 4 }$

Equations and Inequalities

Functions and Graphs

Polynomial and Rational Functions

Systems of Equations and Inequalities

Filters

Exam 4: Exponential and Logarithmic Functions

Write the equation in its equivalent logarithmic form. - b3=2744b ^ { 3 } = 2744b3=2744

Find the domain of the logarithmic function. - f(x)=log⁡5(x−2)2f ( x ) = \log _ { 5 } ( x - 2 ) ^ { 2 }f(x)=log5​(x−2)2

The graph of a logarithmic function is given. Select the function for the graph from the options. -

Evaluate the expression without using a calculator. - log⁡273\log _ { 27 } 3log27​3

Graph the function. -Use the graph of f(x)=4xf ( x ) = 4 ^ { x }f(x)=4x to obtain the graph of g(x)=4−xg ( x ) = 4 ^ { - x }g(x)=4−x .

Graph the functions in the same rectangular coordinate system. - f(x)=3x and g(x)=log⁡3xf(x)=3^{x} \text { and } g(x)=\log _{3} xf(x)=3x and g(x)=log3​x

Graph the function. -Use the graph of log⁡5x\log _ { 5 } xlog5​x to obtain the graph of f(x)=12log⁡5xf ( x ) = \frac { 1 } { 2 } \log _ { 5 } xf(x)=21​log5​x .

Write the equation in its equivalent logarithmic form. - 53=x5 ^ { 3 } = x53=x

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - ln⁡(e29)\ln \left( \frac { e ^ { 2 } } { 9 } \right)ln(9e2​)

Approximate the number using a calculator. Round your answer to three decimal places. - 272^{ \sqrt { 7 }}27​

Graph the function. -Use the graph of f(x)=exf ( x ) = e ^ { x }f(x)=ex to obtain the graph of g(x)=ex/4+3g ( x ) = e ^ { x / 4 } + 3g(x)=ex/4+3 .

Graph the function by making a table of coordinates - f(x)=4xf ( x ) = 4 ^ { x }f(x)=4x

Graph the function. -Use the graph of f(x)=2xf ( x ) = 2 ^ { x }f(x)=2x to obtain the graph of g(x)=2x−3g ( x ) = 2 ^ { x - 3 }g(x)=2x−3

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - log⁡5(125x−1)\log _ { 5 } \left( \frac { 125 } { \sqrt { x - 1 } } \right)log5​(x−1​125​)

The graph of a logarithmic function is given. Select the function for the graph from the options. -

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - ln⁡ey3\ln \sqrt [ 3 ] { \mathrm { ey } }ln3ey​

Evaluate the expression without using a calculator. - log⁡214\log _ { 2 } \frac { 1 } { 4 }log2​41​

Equations and Inequalities

Functions and Graphs

Polynomial and Rational Functions

Systems of Equations and Inequalities

Filters

Write the equation in its equivalent logarithmic form. - $b ^ { 3 } = 2744$

Find the domain of the logarithmic function. - $f ( x ) = \log _ { 5 } ( x - 2 ) ^ { 2 }$

Evaluate the expression without using a calculator. - $\log _ { 27 } 3$

Graph the function. -Use the graph of $f ( x ) = 4 ^ { x }$ to obtain the graph of $g ( x ) = 4 ^ { - x }$ . $Graph the function. -Use the graph of f ( x ) = 4 ^ { x } to obtain the graph of g ( x ) = 4 ^ { - x } .$

Graph the functions in the same rectangular coordinate system. - $f(x)=3^{x} \text { and } g(x)=\log _{3} x$ $Graph the functions in the same rectangular coordinate system. - f(x)=3^{x} \text { and } g(x)=\log _{3} x$

Graph the function. -Use the graph of $\log _ { 5 } x$ to obtain the graph of $f ( x ) = \frac { 1 } { 2 } \log _ { 5 } x$ . $Graph the function. -Use the graph of \log _ { 5 } x to obtain the graph of f ( x ) = \frac { 1 } { 2 } \log _ { 5 } x .$

Write the equation in its equivalent logarithmic form. - $5 ^ { 3 } = x$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\ln \left( \frac { e ^ { 2 } } { 9 } \right)$

Approximate the number using a calculator. Round your answer to three decimal places. - $2^{ \sqrt { 7 }}$

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = e ^ { x / 4 } + 3$ . $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = e ^ { x / 4 } + 3 .$

Graph the function by making a table of coordinates - $f ( x ) = 4 ^ { x }$ $Graph the function by making a table of coordinates - f ( x ) = 4 ^ { x }$

Graph the function. -Use the graph of $f ( x ) = 2 ^ { x }$ to obtain the graph of $g ( x ) = 2 ^ { x - 3 }$ $Graph the function. -Use the graph of f ( x ) = 2 ^ { x } to obtain the graph of g ( x ) = 2 ^ { x - 3 }$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log _ { 5 } \left( \frac { 125 } { \sqrt { x - 1 } } \right)$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\ln \sqrt [ 3 ] { \mathrm { ey } }$

Evaluate the expression without using a calculator. - $\log _ { 2 } \frac { 1 } { 4 }$