Exam 4: Exponential and Logarithmic Functions

Solve the problem. -The function $\mathrm { f } ( \mathrm { x } ) = 1 + 1.5 \ln ( \mathrm { x } + 1 )$ models the average number of free-throws a basketball player can make consecutively during practice as a function of time, where $x$ is the number of consecutive days the basketball player has practiced for two hours. After 206 days of practice, what is the average number of consecutive free throws the basketball player makes?

(Multiple Choice)

4.8/5

(40)

Question 121

Approximate the number using a calculator. Round your answer to three decimal places. - $2 ^{- 3.3}$

(Multiple Choice)

4.9/5

(41)

Question 122

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log _ { 6 } ( 7 \cdot 3 )$

(Multiple Choice)

4.7/5

(37)

Question 123

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log X ^ { - 2 }$

(Multiple Choice)

4.8/5

(46)

Question 124

Graph the function. -Use the graph of $f ( x ) = 4 ^ { x }$ to obtain the graph of $g ( x ) = 4 \cdot 4 ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = 4 ^ { x } to obtain the graph of g ( x ) = 4 \cdot 4 ^ { x } .$

(Multiple Choice)

4.9/5

(33)

Question 125

Write the equation in its equivalent exponential form. - $\log _ { \mathrm { b } } 64 = 3$

(Multiple Choice)

4.9/5

(26)

Question 126

Evaluate the expression without using a calculator. - $\log _ { 4 } 64$

(Multiple Choice)

4.8/5

(35)

Question 127

Graph the function by making a table of coordinates - $f(x)=\left(\frac{4}{3}\right)^{x}$ $Graph the function by making a table of coordinates - f(x)=\left(\frac{4}{3}\right)^{x}$

(Multiple Choice)

4.8/5

(32)

Question 128

Graph the function. -Use the graph of $f ( x ) = 2 ^ { x }$ to obtain the graph of $g ( x ) = - 2 ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = 2 ^ { x } to obtain the graph of g ( x ) = - 2 ^ { x } .$

(Multiple Choice)

4.9/5

(44)

Question 129

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = e ^ { x - 3 } - 1$ $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = e ^ { x - 3 } - 1$

(Multiple Choice)

4.7/5

(39)

Question 130

Write the equation in its equivalent logarithmic form. - $7 ^ { x } = 343$

(Multiple Choice)

4.7/5

(26)

Question 131

Evaluate or simplify the expression without using a calculator. - $9 \log 10 ^ { 6.2 }$

(Multiple Choice)

4.8/5

(35)

Question 132

Graph the function. -Use the graph of $f ( x ) = \ln x$ to obtain the graph of $g ( x ) = 4 - \ln x$ . $Graph the function. -Use the graph of f ( x ) = \ln x to obtain the graph of g ( x ) = 4 - \ln x .$

(Multiple Choice)

4.8/5

(23)

Question 133

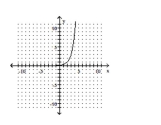
The graph of an exponential function is given. Select the function for the graph from the functions listed. -

(Multiple Choice)

4.8/5

(29)

Question 134

Find the domain of the logarithmic function. - $f ( x ) = \log \left( x ^ { 2 } - 7 x + 12 \right)$

(Multiple Choice)

4.9/5

(43)

Question 135

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = \frac { 1 } { 2 } e ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = \frac { 1 } { 2 } e ^ { x } .$

(Multiple Choice)

4.8/5

(20)

Question 136

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = e ^ { x - 2 }$ . $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = e ^ { x - 2 } .$

(Multiple Choice)

4.9/5

(38)

Question 137

Write the equation in its equivalent logarithmic form. - $5 ^ { 2 } = 25$

(Multiple Choice)

4.8/5

(30)

Question 138

Graph the function. -Use the graph of $f ( x ) = 5 ^ { x }$ to obtain the graph of $g ( x ) = \frac { 1 } { 5 } \cdot 5 ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = 5 ^ { x } to obtain the graph of g ( x ) = \frac { 1 } { 5 } \cdot 5 ^ { x } .$

(Multiple Choice)

4.7/5

(41)

Question 139

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log _ { 7 } ( 7 x )$

(Multiple Choice)

4.9/5

(44)

Question 140

Showing 121 - 140 of 146

Approximate the number using a calculator. Round your answer to three decimal places. - $2 ^{- 3.3}$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log _ { 6 } ( 7 \cdot 3 )$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log X ^ { - 2 }$

Graph the function. -Use the graph of $f ( x ) = 4 ^ { x }$ to obtain the graph of $g ( x ) = 4 \cdot 4 ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = 4 ^ { x } to obtain the graph of g ( x ) = 4 \cdot 4 ^ { x } .$

Write the equation in its equivalent exponential form. - $\log _ { \mathrm { b } } 64 = 3$

Evaluate the expression without using a calculator. - $\log _ { 4 } 64$

Graph the function by making a table of coordinates - $f(x)=\left(\frac{4}{3}\right)^{x}$ $Graph the function by making a table of coordinates - f(x)=\left(\frac{4}{3}\right)^{x}$

Graph the function. -Use the graph of $f ( x ) = 2 ^ { x }$ to obtain the graph of $g ( x ) = - 2 ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = 2 ^ { x } to obtain the graph of g ( x ) = - 2 ^ { x } .$

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = e ^ { x - 3 } - 1$ $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = e ^ { x - 3 } - 1$

Write the equation in its equivalent logarithmic form. - $7 ^ { x } = 343$

Evaluate or simplify the expression without using a calculator. - $9 \log 10 ^ { 6.2 }$

Graph the function. -Use the graph of $f ( x ) = \ln x$ to obtain the graph of $g ( x ) = 4 - \ln x$ . $Graph the function. -Use the graph of f ( x ) = \ln x to obtain the graph of g ( x ) = 4 - \ln x .$

The graph of an exponential function is given. Select the function for the graph from the functions listed. -

Find the domain of the logarithmic function. - $f ( x ) = \log \left( x ^ { 2 } - 7 x + 12 \right)$

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = \frac { 1 } { 2 } e ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = \frac { 1 } { 2 } e ^ { x } .$

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = e ^ { x - 2 }$ . $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = e ^ { x - 2 } .$

Write the equation in its equivalent logarithmic form. - $5 ^ { 2 } = 25$

Graph the function. -Use the graph of $f ( x ) = 5 ^ { x }$ to obtain the graph of $g ( x ) = \frac { 1 } { 5 } \cdot 5 ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = 5 ^ { x } to obtain the graph of g ( x ) = \frac { 1 } { 5 } \cdot 5 ^ { x } .$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log _ { 7 } ( 7 x )$

Equations and Inequalities

Functions and Graphs

Polynomial and Rational Functions

Systems of Equations and Inequalities

Filters

Exam 4: Exponential and Logarithmic Functions

Approximate the number using a calculator. Round your answer to three decimal places. - 2−3.32 ^{- 3.3}2−3.3

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - log⁡6(7⋅3)\log _ { 6 } ( 7 \cdot 3 )log6​(7⋅3)

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - log⁡X−2\log X ^ { - 2 }logX−2

Graph the function. -Use the graph of f(x)=4xf ( x ) = 4 ^ { x }f(x)=4x to obtain the graph of g(x)=4⋅4xg ( x ) = 4 \cdot 4 ^ { x }g(x)=4⋅4x .

Write the equation in its equivalent exponential form. - log⁡b64=3\log _ { \mathrm { b } } 64 = 3logb​64=3

Evaluate the expression without using a calculator. - log⁡464\log _ { 4 } 64log4​64

Graph the function by making a table of coordinates - f(x)=(43)xf(x)=\left(\frac{4}{3}\right)^{x}f(x)=(34​)x

Graph the function. -Use the graph of f(x)=2xf ( x ) = 2 ^ { x }f(x)=2x to obtain the graph of g(x)=−2xg ( x ) = - 2 ^ { x }g(x)=−2x .

Graph the function. -Use the graph of f(x)=exf ( x ) = e ^ { x }f(x)=ex to obtain the graph of g(x)=ex−3−1g ( x ) = e ^ { x - 3 } - 1g(x)=ex−3−1

Write the equation in its equivalent logarithmic form. - 7x=3437 ^ { x } = 3437x=343

Evaluate or simplify the expression without using a calculator. - 9log⁡106.29 \log 10 ^ { 6.2 }9log106.2

Graph the function. -Use the graph of f(x)=ln⁡xf ( x ) = \ln xf(x)=lnx to obtain the graph of g(x)=4−ln⁡xg ( x ) = 4 - \ln xg(x)=4−lnx .

The graph of an exponential function is given. Select the function for the graph from the functions listed. -

Find the domain of the logarithmic function. - f(x)=log⁡(x2−7x+12)f ( x ) = \log \left( x ^ { 2 } - 7 x + 12 \right)f(x)=log(x2−7x+12)

Graph the function. -Use the graph of f(x)=exf ( x ) = e ^ { x }f(x)=ex to obtain the graph of g(x)=12exg ( x ) = \frac { 1 } { 2 } e ^ { x }g(x)=21​ex .

Graph the function. -Use the graph of f(x)=exf ( x ) = e ^ { x }f(x)=ex to obtain the graph of g(x)=ex−2g ( x ) = e ^ { x - 2 }g(x)=ex−2 .

Write the equation in its equivalent logarithmic form. - 52=255 ^ { 2 } = 2552=25

Graph the function. -Use the graph of f(x)=5xf ( x ) = 5 ^ { x }f(x)=5x to obtain the graph of g(x)=15⋅5xg ( x ) = \frac { 1 } { 5 } \cdot 5 ^ { x }g(x)=51​⋅5x .

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - log⁡7(7x)\log _ { 7 } ( 7 x )log7​(7x)

Equations and Inequalities

Functions and Graphs

Polynomial and Rational Functions

Systems of Equations and Inequalities

Filters

Approximate the number using a calculator. Round your answer to three decimal places. - $2 ^{- 3.3}$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log _ { 6 } ( 7 \cdot 3 )$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log X ^ { - 2 }$

Graph the function. -Use the graph of $f ( x ) = 4 ^ { x }$ to obtain the graph of $g ( x ) = 4 \cdot 4 ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = 4 ^ { x } to obtain the graph of g ( x ) = 4 \cdot 4 ^ { x } .$

Write the equation in its equivalent exponential form. - $\log _ { \mathrm { b } } 64 = 3$

Evaluate the expression without using a calculator. - $\log _ { 4 } 64$

Graph the function by making a table of coordinates - $f(x)=\left(\frac{4}{3}\right)^{x}$ $Graph the function by making a table of coordinates - f(x)=\left(\frac{4}{3}\right)^{x}$

Graph the function. -Use the graph of $f ( x ) = 2 ^ { x }$ to obtain the graph of $g ( x ) = - 2 ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = 2 ^ { x } to obtain the graph of g ( x ) = - 2 ^ { x } .$

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = e ^ { x - 3 } - 1$ $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = e ^ { x - 3 } - 1$

Write the equation in its equivalent logarithmic form. - $7 ^ { x } = 343$

Evaluate or simplify the expression without using a calculator. - $9 \log 10 ^ { 6.2 }$

Graph the function. -Use the graph of $f ( x ) = \ln x$ to obtain the graph of $g ( x ) = 4 - \ln x$ . $Graph the function. -Use the graph of f ( x ) = \ln x to obtain the graph of g ( x ) = 4 - \ln x .$

Find the domain of the logarithmic function. - $f ( x ) = \log \left( x ^ { 2 } - 7 x + 12 \right)$

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = \frac { 1 } { 2 } e ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = \frac { 1 } { 2 } e ^ { x } .$

Graph the function. -Use the graph of $f ( x ) = e ^ { x }$ to obtain the graph of $g ( x ) = e ^ { x - 2 }$ . $Graph the function. -Use the graph of f ( x ) = e ^ { x } to obtain the graph of g ( x ) = e ^ { x - 2 } .$

Write the equation in its equivalent logarithmic form. - $5 ^ { 2 } = 25$

Graph the function. -Use the graph of $f ( x ) = 5 ^ { x }$ to obtain the graph of $g ( x ) = \frac { 1 } { 5 } \cdot 5 ^ { x }$ . $Graph the function. -Use the graph of f ( x ) = 5 ^ { x } to obtain the graph of g ( x ) = \frac { 1 } { 5 } \cdot 5 ^ { x } .$

Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. - $\log _ { 7 } ( 7 x )$