Exam 5: Analytic Trigonometry
Exam 1: Functions and Graphs50 Questions
Exam 2: Polynomial, Power, and Rational Functions52 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions52 Questions
Exam 4: Trigonometric Functions50 Questions
Exam 5: Analytic Trigonometry50 Questions
Exam 6: Applications of Trigonometry52 Questions
Exam 7: Systems and Matrices50 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions52 Questions
Exam 9: Discrete Mathematics62 Questions
Exam 10: An Introduction to Calculus: Limits, Derivatives, and Integrals37 Questions
Exam 11: P Prerequisites52 Questions
Exam 12: Mathematical Problem Set128 Questions
Select questions type
Find all solutions of the equation on the interval (Your answer should be exact.)
Free
(Short Answer)
4.8/5  (36)
(36)
Correct Answer:
A golf ball is hit with initial velocity (in feet per second) and trajectory angle The horizontal distance traveled before it bounces is given by
Find the angle of trajectory needed to hit a green 800 feet away on the first bounce if the initial velocity is 200 ft/sec
Free
(Essay)
4.9/5  (35)
(35)
Correct Answer:
The angles of elevation to the top of a tower from two points that are on the same side of the tower and 30 meters apart are and What is the height of the tower?
(Short Answer)
4.7/5  (33)
(33)
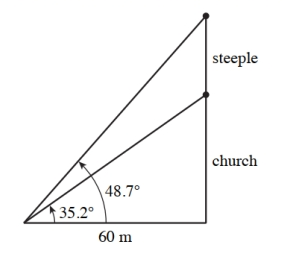
The angle of elevation to the bottom of a steeple of a church is and the angle of elevation to the top of the steeple is . If the angles of elevation are measured from a point on the ground 60 meters from the church steeple, what is the height of the steeple?
(Short Answer)
4.9/5  (26)
(26)
Use the grapher to determine which of the following is an identity.
(Multiple Choice)
4.8/5  (39)
(39)
Use the fundamental identities to change the expression to one involving only sines and cosines. Then simplify. Show all your steps.
(Essay)
4.8/5  (32)
(32)
Use a power-reduction formula to find the exact value (Hint: What is =?)
(Short Answer)
4.8/5  (31)
(31)
Use a sum or difference identity to find the exact value of cos
(Short Answer)
4.8/5  (34)
(34)
Randy must find the distance between points B and C on opposite sides of a lake. He locates a point A that is 385ft from B and 546 ft from C . If the angle at A is what is the distance BC ?
(Short Answer)
4.7/5  (35)
(35)
A golf ball is hit with initial velocity (in feet per second) and trajectory angle The horizontal distance traveled before it bounces is given by Find the angle of trajectory needed to hit a green 700 feet away on the first bounce if the initial velocity is 170 ft/sec.
(Essay)
4.8/5  (38)
(38)
Showing 1 - 20 of 50
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)