Exam 9: Exponential and Logarithmic Functions
Exam 1: Real Numbers and Algebraic Expressions409 Questions
Exam 2: Equations, Inequalities, and Problem Solving282 Questions
Exam 3: Graphs and Functions388 Questions
Exam 4: Systems of Equations and Inequalities131 Questions
Exam 5: Polynomials and Polynomial Functions390 Questions
Exam 6: Rational Expressions292 Questions
Exam 7: Rational Exponents, Radicals, and Complex Numbers382 Questions
Exam 8: Quadratic Equations and Functions251 Questions
Exam 9: Exponential and Logarithmic Functions300 Questions
Exam 10: Conic Sections132 Questions
Exam 11: Fractions134 Questions
Select questions type
Solve.
-Calculate how much money Ronnie has after 3 years if he originally invested at compounded continuously. Use , where is the final amount, is the original amount deposited, is the interest rate, and is the number of years.
(Multiple Choice)
4.9/5  (34)
(34)
Solve. Round the answer to the nearest whole.
-The size of the rat population of a wharf area grows at a rate of 7% monthly. If there are 300 rats in June, find how many rats should be expected by next June.
(Multiple Choice)
4.7/5  (32)
(32)
Determine whether the function is a one-to-one function.
-
(Multiple Choice)
5.0/5  (29)
(29)
Determine whether the function is a one-to-one function.
-
(Multiple Choice)
4.8/5  (34)
(34)
Graph the function and its inverse on the same set of axes.
-
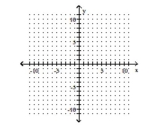
(Multiple Choice)
4.9/5  (33)
(33)
For the given functions f and g, find the composition.
-
Find .
(Multiple Choice)
4.8/5  (31)
(31)
Graph the function and its inverse on the same set of axes.
-
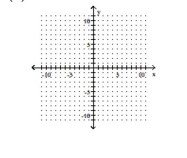
(Multiple Choice)
4.9/5  (30)
(30)
Use a calculator to approximate the logarithm to four decimal places.
-
(Multiple Choice)
4.8/5  (41)
(41)
Use the following approximations to find the approximate value of the logarithmic expression: logb
logb
-
(Multiple Choice)
4.9/5  (26)
(26)
Solve.
-A city is growing at the rate of 0.8% annually. If there were 3,917,000 residents in the city in 1994, find how many (to the nearest ten-thousand) are living in that city in 2000
(Multiple Choice)
4.8/5  (36)
(36)
Write the function F(x) as a composition of f, g, or h.
- f(x)=+6g(x)=7xh(x)= F(x)=
(Multiple Choice)
4.8/5  (42)
(42)
Express as the logarithm of a single expression. Assume that variables represent positive numbers.
-
(Multiple Choice)
4.8/5  (36)
(36)
Use the exponential decay formula with half-lives to find the final amount. Round to the nearest tenth when necessary.
- Original Amount Half-Life (in years) Number of Years Final Amount after x Time Intervals 500 15 45
(Multiple Choice)
4.9/5  (27)
(27)
Showing 181 - 200 of 300
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)