Exam 5: Induction and Recursion
Exam 1: The Foundations: Logic and Proofs200 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices214 Questions
Exam 3: Algorithms52 Questions
Exam 4: Number Theory and Cryptography154 Questions
Exam 5: Induction and Recursion53 Questions
Exam 6: Counting156 Questions
Exam 7: Discrete Probability53 Questions
Exam 8: Advanced Counting Techniques128 Questions
Exam 9: Relations74 Questions
Exam 10: Graphs127 Questions
Exam 11: Trees97 Questions
Exam 12: Boolean Algebra77 Questions
Exam 13: Modeling Computation71 Questions
Select questions type
In questions give a recursive definition with initial condition(s).
-The function
(Short Answer)
4.9/5  (33)
(33)
Use mathematical induction to show that n lines in the plane passing through the same point divide the plane
into
(Short Answer)
4.8/5  (42)
(42)
In questions give a recursive definition with initial condition(s).
-The set
(Short Answer)
4.9/5  (37)
(37)
Consider the following program segment: i:=1 total :=1 while i invariant.
(Short Answer)
4.8/5  (38)
(38)
In questions give a recursive definition with initial condition(s) of the set S.
-
(Short Answer)
4.8/5  (45)
(45)
Verify that the program segment a:=2 b:=a+c is correct with respect to the initial assertion c = 3 and the final assertion b = 5.
(Short Answer)
5.0/5  (38)
(38)
A T -omino is a tile pictured at the right. Prove that every chessboard can be tiled with T-ominoes.
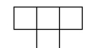
(Short Answer)
4.9/5  (37)
(37)
Use mathematical induction to prove that every integer amount of postage of six cents or more can be formed
using 3-cent and 4-cent stamps.
(Short Answer)
4.8/5  (28)
(28)
In questions give a recursive definition with initial condition(s).
-The set
(Short Answer)
5.0/5  (43)
(43)
In questions give a recursive definition with initial condition(s).
-The set
(Short Answer)
4.8/5  (37)
(37)
Verify that the following program segment is correct with respect to the initial assertion T and the final
assertion (x ≤ y ∧ max = y) ∨ (x > y ∧ max = x):
if x ≤ y then
max := y
else
max := x
(Essay)
4.8/5  (34)
(34)
In questions give a recursive definition with initial condition(s) of the set S.
-All positive integer multiples of 5.
(Short Answer)
4.8/5  (38)
(38)
In questions give a recursive definition with initial condition(s).
-The sequence
(Short Answer)
4.8/5  (37)
(37)
Suppose you wish to use the Principle of Mathematical Induction to prove that
(a) Write P(1)
(b) Write P(5)
(c) Write P(k)
(d) Write P(k+1)
(e) Use the Principle of Mathematical Induction to prove that P(n) is true for all
(Short Answer)
4.8/5  (33)
(33)
Showing 21 - 40 of 53
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)