Exam 7: Analytic Geometry
Exam 1: Equations and Inequalities296 Questions
Exam 2: Functions and Relations380 Questions
Exam 3: Polynomial and Rational Functions300 Questions
Exam 4: Exponential and Logarithmic Functions314 Questions
Exam 5: Systems of Equations and Inequalities215 Questions
Exam 6: Matrices and Determinants and Applications154 Questions
Exam 7: Analytic Geometry131 Questions
Exam 8: Sequences, Series, Induction, and Probability270 Questions
Exam 9: Review of Prerequisites226 Questions
Select questions type
An equation of a parabola is given. Graph the parabola. Identify the vertex and the
focal diameter.
-
(Multiple Choice)
4.8/5  (36)
(36)
An equation of a parabola is given. Write the equation of the parabola in standard form, and identify the
vertex and the focal diameter.
-
(Multiple Choice)
5.0/5  (34)
(34)
Solve the problem.
- Radio signals emitted from points (10, 0) and (-10, 0) indicate that a plane is 8 miles closer to (10,0) than to (-10, 0). Find an equation of the hyperbola that passes through the plane's location with foci (10, 0) and (-10, 0). All units are in miles.
Radio signals emitted from points (0, 8) and (0, -8) indicate that a plane is 4 miles farther from (0, 8) than (0, -8). Find an equation of the hyperbola that passes through the plane's location with foci (0,8) and (0, -8).
From the figure, the plane is located in the fourth quadrant of the coordinate system. Solve the system of equations defining the two hyperbolas for the point of intersection in the fourth quadrant. This is the location o the plane.
Round the coordinates to the nearest tenth of a mile.
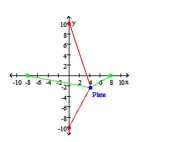
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-a. A circular vent pipe with diameter 4 inches is placed on a flat roof. Write an equation of the circular cross section that the pipe makes with the roof. Assume the origin is placed at the center of The circle.
b. Suppose the pipe is instead placed on a roof with a slope of . The cross-section of the pipe Where it intersects the roof is an ellipse. Determine the lengths of the major and minor axes of this Ellipse.
(Multiple Choice)
4.9/5  (33)
(33)
An________ is a set of points (x, y) in a plane such that the sum of the distances between (x, y) and two fixed points called________ is a constant.
(Short Answer)
4.8/5  (36)
(36)
The circle, the ellipse, the hyperbola, and the parabola are categories of ________sections.
(Short Answer)
4.8/5  (33)
(33)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-The line segment perpendicular to the transverse axis passing through the center of a hyperbola, and with endpoints on the reference rectangle is called the ________axis.
(Short Answer)
4.8/5  (34)
(34)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-Given ), the ordered pairs representing the vertex and focus are________ and________, respectively. The directrix is the line defined by the equation________ .
(Short Answer)
4.7/5  (44)
(44)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-The points where a hyperbola intersects the line through the foci are called the ________.
(Short Answer)
4.9/5  (22)
(22)
Given an ellipse with major axis of length 2a and minor axis of length 2b, the area is given by A =ab.
The perimeter is approximated by a. Determine the area of the ellipse. b. Approximate the perimeter.
-
(Multiple Choice)
4.7/5  (43)
(43)
Write the equation of the ellipse in standard form. Identify the vertices and foci.
-
(Multiple Choice)
4.7/5  (39)
(39)
The line through the foci intersects an ellipse at two points called________ .
(Short Answer)
4.8/5  (31)
(31)
Solve the problem.
-A 20-in. satellite dish for a television has parabolic cross sections. A coordinate system is chosen so that the vertex of a cross section through the center of the dish is located at (0, 0). The equation of
The parabola is modeled by where x and y are measured in inches. Where should the
Receiver be placed to maximize signal strength? That is, where is the focus?
(Multiple Choice)
4.7/5  (46)
(46)
Solve the problem.
-A planet's moon has an orbit that is elliptical with eccentricity 0.054 and with the planet at one focus. If the distance between the moon and the planet at perihelion (the closest point) is 364,100
Km, determine the distance at aphelion (the farthest point). Round to the nearest 100 km.
(Multiple Choice)
4.9/5  (24)
(24)
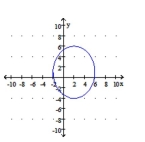
Find the standard form of the equation of the ellipse or hyperbola shown.
-
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-A homeowner wants to make an elliptical rug from a 30-foot by 10-foot rectangular piece of carpeting.
a. What lengths of the major and minor axes would maximize the area of the new rug?
b. Write an equation of the ellipse with maximum area. Use a coordinate system with the origin at the center
Of the rug and horizontal major axis.
(Multiple Choice)
4.7/5  (31)
(31)
Write the equation of the ellipse in standard form. Identify the vertices and foci.
-
(Multiple Choice)
4.9/5  (43)
(43)
Showing 61 - 80 of 131
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)