Exam 6: Matrices and Determinants and Applications
Exam 1: Equations and Inequalities296 Questions
Exam 2: Functions and Relations380 Questions
Exam 3: Polynomial and Rational Functions300 Questions
Exam 4: Exponential and Logarithmic Functions314 Questions
Exam 5: Systems of Equations and Inequalities215 Questions
Exam 6: Matrices and Determinants and Applications154 Questions
Exam 7: Analytic Geometry131 Questions
Exam 8: Sequences, Series, Induction, and Probability270 Questions
Exam 9: Review of Prerequisites226 Questions
Select questions type
Write the system of equations as a matrix equation of the form AX = B, where A is the coefficient matrix, X is the column matrix of variables, and B is the column matrix of constants.
- -5x-8y+9z=16 2x-z=5 -7y+z=8
(Multiple Choice)
4.7/5  (35)
(35)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-True or false? A system of linear equations in three variables may have exactly two solutions.
(True/False)
4.7/5  (31)
(31)
Solve the problem.
-Danielle stayed in three different cities (Washington, D.C., Atlanta, Georgia, and Dallas, Texas) for a total of 22 nights. She spent twice as many nights in Dallas as she did in Washington. The total
Cost for 22 nights (excluding tax) was $3,100. Determine the number of nights that she spent in each city. City Cost per Night Washington \ 100 Atlanta \ 175 Dallas \ 150
(Multiple Choice)
4.9/5  (44)
(44)
Use a calculator to approximate the reduced row-echelon form of the augmented matrix representing the
given system. Give the solution set where x, y, and z are rounded to 2 decimal places.
- 0.52x-3.79y-4.67z =9.15 0.03x+0.06y+0.13z =0.53 0.974x+0.813y+0.419z =0.189
(Multiple Choice)
4.9/5  (27)
(27)
Write the word or phrase that best completes each statement or answers the question.
Solve the problem.
-Assume that traffic flows freely through intersections A, B, and C. The values , and all other
numbers in the figure represent flow rates in vehicles per hour. 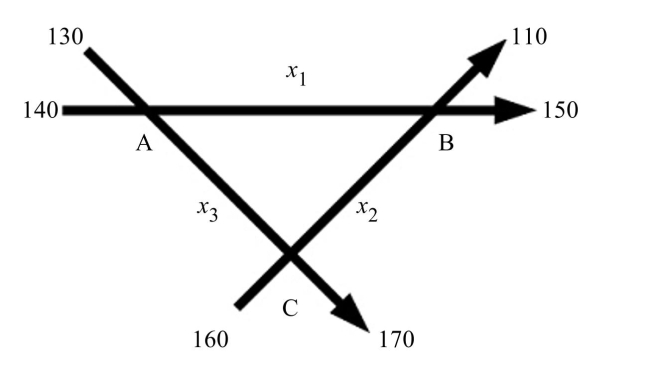 a. Write an equation representing equal flow into and out of intersection A.
b. Write an equation representing equal flow into and out of intersection B.
c. Write an equation representing equal flow into and out of intersection C.
d. Write the system of equations from parts (a)-(c) in standard form.
e. Write the reduced row-echelon form of the augmented matrix representing the system of equations from
part (d).
f. If the flow rate between intersections A and C is 120 vehicles per hour, determine the flow rates and g. If the flow rate between intersections A and C is between 150 and 240 vehicles per hour, inclusive,
determine the flow rates
a. Write an equation representing equal flow into and out of intersection A.
b. Write an equation representing equal flow into and out of intersection B.
c. Write an equation representing equal flow into and out of intersection C.
d. Write the system of equations from parts (a)-(c) in standard form.
e. Write the reduced row-echelon form of the augmented matrix representing the system of equations from
part (d).
f. If the flow rate between intersections A and C is 120 vehicles per hour, determine the flow rates and g. If the flow rate between intersections A and C is between 150 and 240 vehicles per hour, inclusive,
determine the flow rates
(Short Answer)
4.8/5  (31)
(31)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-True or false? A system of linear equations in three variables may have infinitely many solutions.
(True/False)
4.9/5  (29)
(29)
Choose the one alternative that best completes the statement or answers the question.
Write the augmented matrix for the given system.
- 7x+9 =-7z -4x+4z =-8-6y -3x-7y+9z =2
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-A student researches the cost for three cell phone plans. Matrix C contains the cost per text message and the cost per minute over the maximum number of minutes allowed in each plan. Matrix N
Represents the number of text messages and number of minutes over the maximum for 3 months.
Month 1 Month 2 Month 3
Nequals open bracket 27 60 25 105 27 0 close bracket Number of texts Minutes over
Find the product and interpret its meaning.
(Multiple Choice)
4.8/5  (31)
(31)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-If the ________of a matrix is , then p represents the number of________ and q represents the number of .
(Short Answer)
4.9/5  (39)
(39)
Solve the problem.
-In matrix C, a coffee shop records the cost to produce a cup of coffee and the cost to produce a cup of hot chocolate. Matrix P contains the selling prices to the customer. coffee chocolate C= \ 0.93 \ 0.86 \ 1.21 \ 1.11 \ 1.51 \ 1.41 Small Large coffee chocolate Medium ;P= \ 3.00 \ 2.40 \ 3.75 \ 3.15 \ 4.40 \ 3.90 Sedium Large
a. Compute P - C and interpret its meaning.
b.If the tax rate in a certain city is 6%, use scalar multiplication to find a matrix F that gives the final Price to the customer (including sales tax) for both beverages for each size. Round each entry to the Nearest cent.
(Multiple Choice)
4.7/5  (39)
(39)
Give the order of the matrix. Classify the matrix as a square matrix, row matrix, column matrix, or none
of these.
-
(Multiple Choice)
5.0/5  (32)
(32)
The solution set to a system of dependent equations is given. Write three ordered triples that are
solutions to the system. Answers may vary.
- and are any real numbers
(Multiple Choice)
4.8/5  (30)
(30)
Showing 141 - 154 of 154
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)