Exam 6: Matrices and Determinants and Applications
Exam 1: Equations and Inequalities296 Questions
Exam 2: Functions and Relations380 Questions
Exam 3: Polynomial and Rational Functions300 Questions
Exam 4: Exponential and Logarithmic Functions314 Questions
Exam 5: Systems of Equations and Inequalities215 Questions
Exam 6: Matrices and Determinants and Applications154 Questions
Exam 7: Analytic Geometry131 Questions
Exam 8: Sequences, Series, Induction, and Probability270 Questions
Exam 9: Review of Prerequisites226 Questions
Select questions type
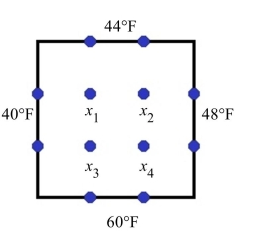
Physicists know that if each edge of a thin conducting plate is kept at a constant temperature, then the
temperature at the interior points is the mean (average) of the four surrounding points equidistant from
the interior point. Use this principle in to find the temperature at points
-
(Multiple Choice)
4.7/5  (36)
(36)
Perform the indicated row operations, then write the new matrix.
- open bracket 1 1 1 -1 -2 3 5 3 3 2 4 1 close bracket 2R1+R2\rightarrowR2, -3R1+R3\rightarrowR3
(Multiple Choice)
4.9/5  (32)
(32)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-A matrix that does not have an inverse is called a ________matrix. A matrix that does have an inverse is said to be invertible or ________.
(Short Answer)
4.8/5  (30)
(30)
Find the partial fraction decomposition for the given rational expression. Use the technique of Gaussian
elimination to find A, B, and C.
-
(Multiple Choice)
4.8/5  (33)
(33)
Find the cofactor of the given element.
- A= = 7 -2 5 2 5 4 -1 -9 3
(Multiple Choice)
4.9/5  (43)
(43)
Solve the system using Gaussian elimination or Gauss-Jordan elimination.
- 2(x-2z)=3y+x+30 x=2y-2z-3 -5x+2y+6z=-41
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-A gas station manager records the number of gallons of Regular, Plus, and Premium gasoline sold during the week (Monday-Friday) and on the weekends (Saturday-Sunday) in matrix A. The selling Price and profit for 1 gal of each type of gasoline is given in matrix B.
Aequals open bracket 4,270 1,760 810 2,320 610 410 close bracket Weekdays Weekend
Selling B= Price Profit \ 3.49 \ 0.26 \ 4.09 \ 0.28 \ 0.20 Regular Plus Premium
a. Compute .
b. Determine the profit for the weekend.
c. Determine the revenue for the entire week.
(Multiple Choice)
4.9/5  (35)
(35)
An________ matrix is used to represent a system of linear equations written in standard form.
(Short Answer)
4.8/5  (30)
(30)
Choose the one alternative that best completes the statement or answers the question.
Evaluate the determinant of the given matrix.
-
(Multiple Choice)
4.9/5  (36)
(36)
Choose the one alternative that best completes the statement or answers the question.
For the given augmented matrix, determine the number of solutions to the corresponding system of
equations.
-
(Multiple Choice)
4.9/5  (32)
(32)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-When applying Cramer's rule, if D = 0, then the system (does / does not) have a unique solution.
(Short Answer)
4.8/5  (32)
(32)
Give the order of the matrix. Classify the matrix as a square matrix, row matrix, column matrix, or none
of these.
-
(Multiple Choice)
4.9/5  (30)
(30)
Choose the one alternative that best completes the statement or answers the question.
Write the augmented matrix for the given system.
- -3x-6y+9z =12 -x+2y =-10 x-8z =-2
(Multiple Choice)
4.8/5  (38)
(38)
Write the word or phrase that best completes each statement or answers the question.
Solve the problem.
-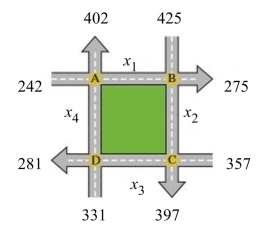 a. Assume that traffic flows at a rate of 215 vehicles per hour on the stretch of road between intersections and . Find the flow rates , and .
b. If traffic flows at a rate of between 195 and 270 vehicles per hour inclusive between intersections and , find the flow rates , and .
a. Assume that traffic flows at a rate of 215 vehicles per hour on the stretch of road between intersections and . Find the flow rates , and .
b. If traffic flows at a rate of between 195 and 270 vehicles per hour inclusive between intersections and , find the flow rates , and .
(Multiple Choice)
4.7/5  (33)
(33)
Solve the system using Gaussian elimination or Gauss-Jordan elimination.
- -6x+15y=15 2x-5y=-5
(Multiple Choice)
4.9/5  (35)
(35)
Determine the inverse of the given matrix, if possible. Otherwise, state the matrix is singular.
-
(Multiple Choice)
4.9/5  (30)
(30)
Showing 61 - 80 of 154
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)