Exam 5: Exponents and Polynomials
Exam 1: Variables, Real Numbers, and Mathematical Models147 Questions
Exam 2: Linear Equations and Inequalities in One Variable181 Questions
Exam 3: Linear Equations in Two Variables121 Questions
Exam 4: Systems of Linear Equations118 Questions
Exam 5: Exponents and Polynomials122 Questions
Exam 6: Factoring Polynomials118 Questions
Exam 7: Rational Expressions135 Questions
Exam 8: Basics of Functions90 Questions
Exam 9: Inequalities and Problem Solving93 Questions
Exam 10: Radicals, Radical Functions, and Rational Exponents102 Questions
Select questions type
Use a vertical format to subtract the polynomials.
- 5+3+2-6 - 2-7+4-5
(Multiple Choice)
4.8/5  (39)
(39)
Perform the indicated operations.
-Subtract -6 - 2x7 + 5x8 - 9x6 + 9x from the sum of -4x6 + 9x + 9 and 9x8 + 4x7.
(Multiple Choice)
4.9/5  (47)
(47)
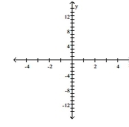
Graph the equation. Find seven solutions in your table of values for the equation by using integers for x, starting with -3
and ending with 3.
-
x +4 -3 -2 -1 0 1 2 3
(Multiple Choice)
4.7/5  (35)
(35)
Find the area of the shaded region. Write the answer as a polynomial in descending powers of x.
-The square garden in the figure measures x yards on each side. The garden is to be expanded so that one side (the top of the figure) is increased by 3 yards and the adjacent side (the right side of the figure) is increased by 1
Yard. Write a polynomial in descending powers of x that expresses the area of the larger garden. Then use the
Polynomial to determine the area of the larger garden if the original garden measures 8 yards on a side. 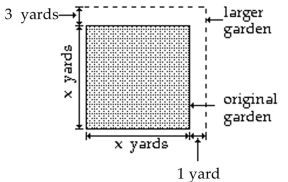
(Multiple Choice)
5.0/5  (30)
(30)
Multiply using the rule for finding the product of the sum and difference of two terms.
-
(Multiple Choice)
4.9/5  (28)
(28)
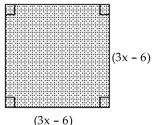
Find the area of the shaded region. Write the answer as a polynomial in descending powers of x.
-
(Multiple Choice)
4.8/5  (35)
(35)
Multiply by using the rule for the square of a binomial.
-
(Multiple Choice)
4.9/5  (37)
(37)
Simplify the expression using the products-to-powers rule.
-
(Multiple Choice)
4.9/5  (35)
(35)
Use the FOIL method to find the product. Express the product in descending powers of the variable.
-
(Multiple Choice)
4.9/5  (33)
(33)
Simplify the expression using the products-to-powers rule.
-
(Multiple Choice)
4.9/5  (40)
(40)
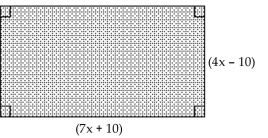
Find the area of the shaded region. Write the answer as a polynomial in descending powers of x.
-
(Multiple Choice)
4.9/5  (40)
(40)
Multiply using the rule for finding the product of the sum and difference of two terms.
-
(Multiple Choice)
4.8/5  (35)
(35)
Multiply by using the rule for the square of a binomial.
-
(Multiple Choice)
4.9/5  (41)
(41)
Showing 101 - 120 of 122
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)