Exam 10: Radicals, Radical Functions, and Rational Exponents
Exam 1: Variables, Real Numbers, and Mathematical Models147 Questions
Exam 2: Linear Equations and Inequalities in One Variable181 Questions
Exam 3: Linear Equations in Two Variables121 Questions
Exam 4: Systems of Linear Equations118 Questions
Exam 5: Exponents and Polynomials122 Questions
Exam 6: Factoring Polynomials118 Questions
Exam 7: Rational Expressions135 Questions
Exam 8: Basics of Functions90 Questions
Exam 9: Inequalities and Problem Solving93 Questions
Exam 10: Radicals, Radical Functions, and Rational Exponents102 Questions
Select questions type
Use the formula for the general term (the nth term) of an arithmetic sequence to find the indicated term of the sequence
with the given first term, a1, and common difference, d.
-Find a 17 when a1 = -4 , d = - 1 .
(Multiple Choice)
4.8/5  (24)
(24)
Write out the first three terms and the last term of the arithmetic sequence.
-
(Multiple Choice)
5.0/5  (34)
(34)
Write the first four terms of the geometric sequence with the given first term, a1, and common ratio, r.
-
(Multiple Choice)
4.8/5  (31)
(31)
Use the formula for the general term (the nth term) of an arithmetic sequence to find the indicated term of the sequence
with the given first term, a1, and common difference, d.
-Find a11 when a1 = 20, d = -6.
(Multiple Choice)
4.8/5  (32)
(32)
Write the first four terms of the geometric sequence with the given first term, a1, and common ratio, r.
-
(Multiple Choice)
5.0/5  (34)
(34)
Write the first five terms of the arithmetic sequence with the given first term, a1, and common difference, d.
-a1 = -36; d = 9
(Multiple Choice)
4.8/5  (42)
(42)
Write the first five terms of the arithmetic sequence with the given first term, a1, and common difference, d.
-a1 = 18; d = -4
(Multiple Choice)
4.8/5  (36)
(36)
Write the first four terms of the geometric sequence with the given first term, a1, and common ratio, r.
-
(Multiple Choice)
4.8/5  (34)
(34)
Find the common ratio for the geometric sequence.
-16, 8, 4, 2, 1, . . .
(Multiple Choice)
4.9/5  (31)
(31)
Use the partial sum formula to find the partial sum of the given arithmetic sequence.
-Find the sum of the first 70 terms of the arithmetic sequence: 1, 8, 15, 22, . . . .
(Multiple Choice)
4.8/5  (28)
(28)
Express the sum using summation notation. Use a lower limit of summation, not necessarily 1, and k for the index of
summation.
-
(Multiple Choice)
4.9/5  (44)
(44)
Solve the problem.
-The bar graph below shows a company's yearly profits from 2003 to 2011. Let an represent the company's profit, in millions, in year n, where n = 1 corresponds to 2003, n = 2 corresponds to 2004, and so on. 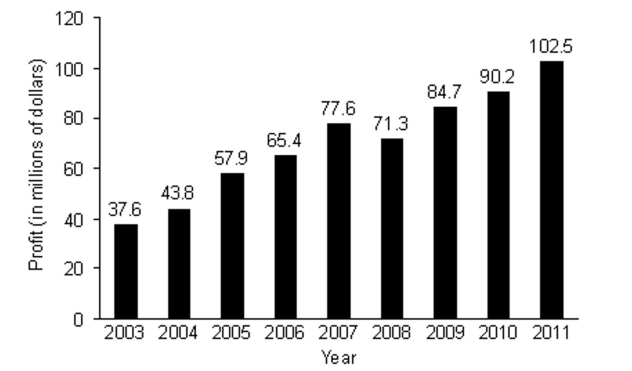
(Multiple Choice)
4.8/5  (38)
(38)
Use the formula for the general term (the nth term) of an arithmetic sequence to find the indicated term of the sequence
with the given first term, a1, and common difference, d.
-Find a 32 when a1 = -3 , d = 3 .
(Multiple Choice)
4.8/5  (36)
(36)
Write the first four terms of the sequence whose general term is given.
-
(Multiple Choice)
4.7/5  (37)
(37)
Solve the problem.
-The population of a town is increasing by 400 inhabitants each year. If its current population is 29,089 and this trend continues, what would its population be in 8 years?
(Multiple Choice)
4.8/5  (32)
(32)
Write a formula for the general term (the nth term) of the arithmetic sequence. Then use the formula for an to find a20,
the 20th term of the sequence.
-
(Multiple Choice)
4.8/5  (44)
(44)
Showing 81 - 100 of 102
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)