Exam 5: Exponential and Logarithmic Functions
Exam 1: Functions, Graphs, and Models; Linear Functions306 Questions
Exam 2: Linear Models, Equations, and Inequalities212 Questions
Exam 3: Quadratic, Piecewise-Defined, and Power Functions261 Questions
Exam 4: Additional Topics With Functions299 Questions
Exam 5: Exponential and Logarithmic Functions304 Questions
Exam 6: Higher-Degree Polynomial and Rational Functions262 Questions
Exam 7: Systems of Equations and Matrices196 Questions
Exam 8: Special Topics in Algebra265 Questions
Select questions type
Provide an appropriate response.
-Select an appropriate type of modeling function for the data shown in the graph. Choose from exponential, logarithmic, and linear. 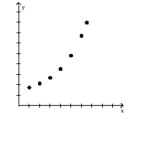
(Multiple Choice)
4.7/5  (32)
(32)
How long would it take $5000 to grow to $25,000 at 9% compounded continuously? Round your answer to the nearest tenth of a year.
(Multiple Choice)
4.7/5  (36)
(36)
In the formula A(t) , A is the amount of radioactive material remaining from an initial amount at a given time t, and k is a negative constant determined by the nature of the material. A certain radioactive isotope
Decays at a rate of 0.125% annually. Determine the half-life of this isotope, to the nearest year.
(Multiple Choice)
4.8/5  (33)
(33)
Provide an appropriate response.
-With the exponential function f(x)
(Essay)
4.8/5  (30)
(30)
Evaluate the function. Round to two decimal places.
-Evaluate
(Multiple Choice)
4.9/5  (38)
(38)
The natural resources of an island limit the growth of the population to a limiting value of 3423. The population of the island is given by the logistic equation where t is the number of years after 2010.
What would be the predicted population of the island in 2019?
(Multiple Choice)
4.8/5  (37)
(37)
The number of students infected with the flu on a college campus after t days is modeled by the function When will the number of infected students be 300?
(Multiple Choice)
4.8/5  (32)
(32)
Evaluate the logarithm, if possible. Round the answer to four decimal places.
-log 169
(Multiple Choice)
4.8/5  (35)
(35)
A certain noise measures 79 decibels. If the intensity is multiplied by 10, how many decibels will the new noise measure?
(Multiple Choice)
4.9/5  (35)
(35)
Evaluate the logarithm, if possible. Round the answer to four decimal places.
-
(Multiple Choice)
4.7/5  (40)
(40)
Find the exponential function that models the data in the table below. x f(x) -2 9 -1 13.5 0 20.25 1 30.375 2 45.5625
(Multiple Choice)
4.9/5  (35)
(35)
Use a change of base formula to evaluate the given logarithm. Approximate to three decimal places.
-
(Multiple Choice)
4.8/5  (38)
(38)
The number of employees of a company, N(t), who have heard a rumor t days after the rumor is started is given by the logistic equation How many employees have heard the rumor 12 days after it is
Started?
(Multiple Choice)
4.9/5  (33)
(33)
Showing 181 - 200 of 304
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)