Exam 3: Quadratic, Piecewise-Defined, and Power Functions
Exam 1: Functions, Graphs, and Models; Linear Functions306 Questions
Exam 2: Linear Models, Equations, and Inequalities212 Questions
Exam 3: Quadratic, Piecewise-Defined, and Power Functions261 Questions
Exam 4: Additional Topics With Functions299 Questions
Exam 5: Exponential and Logarithmic Functions304 Questions
Exam 6: Higher-Degree Polynomial and Rational Functions262 Questions
Exam 7: Systems of Equations and Matrices196 Questions
Exam 8: Special Topics in Algebra265 Questions
Select questions type
Provide an appropriate response.
-Verify that the following data points give constant second differences. Does this guarantee that the points fit
exactly on a quadratic function? Why or why not? x y 1 0 3 3 9 12 27 27 81 48
(Essay)
4.8/5  (29)
(29)
Does it appear that a linear model or a quadratic model is the best fit for the data given in the table below?
Explain your choice. x y 2 25 4 110 6 258 8 472
(Essay)
4.9/5  (42)
(42)
Find a quadratic function that best fits the data. Give answers to the nearest hundredth.
- x -2 5 8 y 5 7 14
(Multiple Choice)
4.9/5  (42)
(42)
Give the coordinates of the vertex and graph the equation in a window that includes the vertex.
-
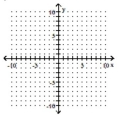
(Multiple Choice)
4.9/5  (43)
(43)
Give the coordinates of the vertex and graph the equation in a window that includes the vertex.
-
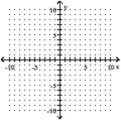
(Multiple Choice)
4.8/5  (36)
(36)
A study in a small town showed that the percent of residents who have college degrees can be modeled by the function where x is the number of years since 2010. Use numerical or graphical methods to find
When the model predicts that the percent will be 70.
(Multiple Choice)
4.8/5  (34)
(34)
Provide an appropriate response.
-If the points in the table lie on a parabola, write the equation whose graph is the parabola. 5 4 3 2 1 0 -24 -9 0 3 0 -9
(Multiple Choice)
4.8/5  (39)
(39)
Use a graphing utility to find or approximate the x-intercepts of the graph of the quadratic function.
-
(Multiple Choice)
4.8/5  (35)
(35)
Determine if the function is increasing or decreasing over the interval indicated.
-
(Multiple Choice)
4.8/5  (35)
(35)
Assume it costs 30 cents to mail a letter weighing one ounce or less, and then 28 cents for each additional ounce or fraction of an ounce. Write a piecewise-defined function P(x) that represents the cost, in cents, of mailing a
Letter weighing between 0 and 3 ounces.
(Multiple Choice)
4.8/5  (27)
(27)
The cumulative number (in thousands) of deaths from a certain disease from 2000 to 2010 may be modeled by , etc. Use the formula for A to estimate symbolically the year when the total number of deaths reached 150 thousand.
(Multiple Choice)
4.8/5  (40)
(40)
Write the equation of the quadratic function whose graph is a parabola containing the given points.
-
(Multiple Choice)
4.8/5  (36)
(36)
Find a power function that models the data in the table. Round to three decimal places if necessary.
- x 2 4 6 8 10 y 6.7 12.1 15.4 18.8 22.7
(Multiple Choice)
4.8/5  (32)
(32)
Use the graph of the function to estimate the x-intercepts.
-
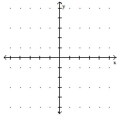
(Multiple Choice)
4.9/5  (35)
(35)
Determine if the graph of the function is concave up or concave down
-
(Multiple Choice)
5.0/5  (36)
(36)
Use a graphing utility to find or approximate solutions to the equation. If necessary, round your answers to three decimal
places.
-
(Multiple Choice)
4.8/5  (32)
(32)
A manufacturer has found that the daily demand for a certain item is , where is the price of the item in dollars. The daily supply is . At what price does supply equal demand? Round your answer to the nearest cent.
(Multiple Choice)
4.8/5  (32)
(32)
Showing 141 - 160 of 261
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)