Exam 7: Applications of Trigonometric Functions
Exam 1: Functions and Their Graphs297 Questions
Exam 2: Linear and Quadratic Functions302 Questions
Exam 3: Polynomial and Rational Functions354 Questions
Exam 4: Exponential and Logarithmic Functions517 Questions
Exam 5: Trigonometric Functions354 Questions
Exam 6: Analytic Trigonometry342 Questions
Exam 7: Applications of Trigonometric Functions105 Questions
Exam 8: Polar Coordinates; Vectors253 Questions
Exam 9: Analytic Geometry200 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability115 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Foundations: a Prelude to Functions234 Questions
Exam 15: Graphing Utilities29 Questions
Select questions type
Two sides of a right triangle ABC (C is the right angle) are given. Find the indicated trigonometric function of the given
angle. Give exact answers with rational denominators.
-Find when and .
(Multiple Choice)
4.9/5  (35)
(35)
An object attached to a coiled spring is pulled down a distance a from its rest position and then released. Assuming that
the motion is simple harmonic with period T, write an equation that relates the displacement d of the object from its rest
position after t seconds. Also assume that the positive direction of the motion is up.
- seconds
(Multiple Choice)
4.7/5  (27)
(27)
Solve the problem.
-Find the area of the Bermuda Triangle if the sides of the triangle have the approximate lengths 844 miles, 921 miles, and 1,314 miles.
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-A guy wire to the top of a tower makes an angle of 64° with the level ground. At a point 26 feet farther from the base of the tower and in line with the base of the wire, the angle of elevation to the top of the tower is . What is the length of the guy wire?
(Multiple Choice)
4.9/5  (29)
(29)
Choose the one alternative that best completes the statement or answers the question.
Find the area of the triangle. If necessary, round the answer to two decimal places.
-a = 4, b = 5, c = 7
(Multiple Choice)
4.8/5  (31)
(31)
Find the area of the triangle. If necessary, round the answer to two decimal places.
-
(Multiple Choice)
4.8/5  (29)
(29)
Choose the one alternative that best completes the statement or answers the question.
-A sailboat leaves port on a bearing of . After sailing for two hours at , the boat turns toward the south. After sailing for three hours at 9 knots on this course, what is the bearing to the ship from port? Round your answer to the nearest .
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-Given a triangle with , what is (are) the possible length(s) of ? Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (38)
(38)
Choose the one alternative that best completes the statement or answers the question.
-It is 4.7 km from Lighthouse A to Port B. The bearing of the port from the lighthouse is N73°E. A ship has sailed due west from the port and its bearing from the lighthouse is N31°E. How far has the ship sailed from the port?
Round your answer to the nearest 0.1 km.
(Multiple Choice)
4.8/5  (30)
(30)
Two sides and an angle are given. Determine whether the given information results in one triangle, two triangles, or no
triangle at all. Solve any triangle(s) that results.
-
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-A room in the shape of a triangle has sides of length , and . If carpeting costs a square yard and padding costs a square yard, how much to the nearest dollar will it cost to carpet the room, assuming that there is no waste?
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-A building 200 feet tall casts a 40 foot long shadow. If a person looks down from the top of the building, what is the measure of the angle between the end of the shadow and the vertical side of the building (to the nearest
Degree)? (Assume the person's eyes are level with the top of the building.)
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-A rocket tracking station has two telescopes A and B placed 1.3 miles apart. The telescopes lock onto a rocket and transmit their angles of elevation to a computer after a rocket launch. What is the distance to the rocket
From telescope B at the moment when both tracking stations are directly east of the rocket telescope A reports an
Angle of elevation of and telescope B reports an angle of elevation of
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-A radio transmission tower is 210 feet tall. How long should a guy wire be if it is to be attached 13 feet from the top and is to make an angle of 20° with the ground? Give your answer to the nearest tenth of a foot.
(Multiple Choice)
4.8/5  (31)
(31)
Choose the one alternative that best completes the statement or answers the question.
Find the exact value of the expression. Do not use a calculator.
-
(Multiple Choice)
4.9/5  (39)
(39)
Write the word or phrase that best completes each statement or answers the question.
-In 1838, the German mathematician and astronomer Friedrich Wilhelm Bessel was the first person to calculate
the distance to a star other than the Sun. He accomplished this by first determining the parallax of the star, 61
Cygni, at 0.314 arc seconds (Parallax is the change in position of the star measured against background stars as
Earth orbits the Sun. See illustration.) If the distance from Earth to the Sun is about 150,000,000 km and
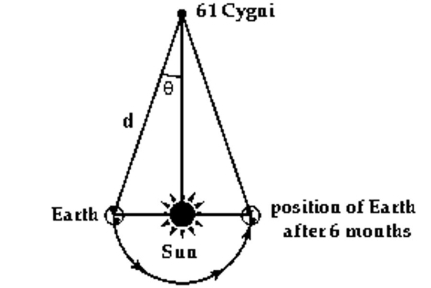
(Essay)
4.9/5  (21)
(21)
Solve the problem.
-John (whose line of sight is 6 ft above horizontal) is trying to estimate the height of a tall oak tree. He first measures the angle of elevation from where he is looking as 35°. He walks 30 feet closer to the tree and finds
That the angle of elevation has increased by 12°. Estimate the height of the tree rounded to the nearest whole
Number.
(Multiple Choice)
4.9/5  (26)
(26)
Two sides of a right triangle ABC (C is the right angle) are given. Find the indicated trigonometric function of the given
angle. Give exact answers with rational denominators.
-Find when and .
(Multiple Choice)
4.9/5  (30)
(30)
Two sides of a right triangle ABC (C is the right angle) are given. Find the indicated trigonometric function of the given
angle. Give exact answers with rational denominators.
-Find when and .
(Multiple Choice)
4.7/5  (35)
(35)
Showing 61 - 80 of 105
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)