Question 1

Find the domain of the function.
-$$f ( x ) = \ln \sqrt { x }$$

Accepted Answer

A)  $( - \infty , 0 )$ 
B)  $( - \infty , 1 )$ 
C)  $( 1 , \infty )$ 
D)  $( 0 , \infty )$ 
A)  $( - \infty , 0 )$ 
B)  $( - \infty , 1 )$ 
C)  $( 1 , \infty )$ 
D)  $( 0 , \infty )$

Question 2

Decide whether or not the functions are inverses of each other.
-$$f ( x ) = 9 x - 9 , g ( x ) = \frac { 1 } { 9 } x + 1$$

Accepted Answer

A)  Yes 
B)  No 
A)  Yes 
B)  No

Question 3

Solve the problem.
-Suppose that $f ( x ) = 3 ^ { x }$. If $f ( x ) = \frac { 1 } { 729 }$, what is $x$ ?

Accepted Answer

A)  6 
B)  $- 2$ 
C)  $- 5$ 
D)  5 
A)  6 
B)  $- 2$ 
C)  $- 5$ 
D)  5

Question 4

Choose the one alternative that best completes the statement or answers the question.
Solve the exponential equation. Use a calculator to obtain a decimal approximation, correct to two decimal places, for the
solution.
-$$4 ^ { x + 7 } = 7$$

Accepted Answer

A)  $\{ 1.56 \}$ 
B)  $\{ - 0.60 \}$ 
C)  $\{ 7.71 \}$ 
D)  $\{ - 5.60 \}$ 
A)  $\{ 1.56 \}$ 
B)  $\{ - 0.60 \}$ 
C)  $\{ 7.71 \}$ 
D)  $\{ - 5.60 \}$

Question 5

Choose the one alternative that best completes the statement or answers the question.
-A grocery store normally sells 8 jars of caviar per week. Use the Poisson Distribution $\mathrm { P } ( \mathrm { x } ) = \frac { 8 ^ { \mathrm { x } } \mathrm { e } ^ { - 8 } } { \mathrm { x } \text { ! } }$ to find the probability (to three decimals) of selling 3 jars in a week. $( x ! = x \cdot ( x - 1 ) \cdot ( x - 2 ) \cdot \ldots \cdot ( 3 ) ( 2 ) ( 1 ) )$.

Accepted Answer

A)  $0.057$ 
B)  $0.019$ 
C)  $0.086$ 
D)  $0.029$ 
A)  $0.057$ 
B)  $0.019$ 
C)  $0.086$ 
D)  $0.029$

Question 6

Decide whether or not the functions are inverses of each other.
-$$f ( x ) = ( x - 6 ) ^ { 2 } , x \geq 6 ; \quad g ( x ) = \sqrt { x + 6 }$$

Accepted Answer

A)  Yes 
B)  $\mathrm { No }$ 
A)  Yes 
B)  $\mathrm { No }$

Question 7

Use a graphing calculator to solve the equation. Round your answer to two decimal places.
-$$e ^ { x } = x ^ { 3 }$$

Accepted Answer

A)  $\{ 1.86 \}$ 
B)  $\{ 2.54 \}$ 
C)  $\{ - 0.71 \}$ 
D)  $\{ - 0.79 \}$ 
A)  $\{ 1.86 \}$ 
B)  $\{ 2.54 \}$ 
C)  $\{ - 0.71 \}$ 
D)  $\{ - 0.79 \}$

Question 8

Choose the one alternative that best completes the statement or answers the question.
-If Emery has $1,100 to invest at 9% per year compounded monthly, how long will it be before he has $1,400? If the compounding is continuous, how long will it be? (Round your answers to three decimal places.)

Accepted Answer

A)  0.036 yrs, 0.268 yrs 
B)  66.89 yrs, 2.902 yrs 
C)  2.69 yrs, 2.68 yrs 
D)  0.233 yrs, 0.223 yrs 
A)  0.036 yrs, 0.268 yrs 
B)  66.89 yrs, 2.902 yrs 
C)  2.69 yrs, 2.68 yrs 
D)  0.233 yrs, 0.223 yrs

Question 9

Find the exact value of the logarithmic expression.
-$\ln \mathrm { e }$

Accepted Answer

A)  1 
B)  e 
C)  0 
D)  $- 1$ 
A)  1 
B)  e 
C)  0 
D)  $- 1$

Question 10

Find the domain of the function.
-$$f ( x ) = \log _ { 10 } \left( \frac { x + 8 } { x - 8 } \right)$$

Accepted Answer

A)  $( 8 , \infty )$ 
B)  $( - \infty , - 8 ) \cup ( 8 , \infty )$ 
C)  $( - \infty , - 8 )$ 
D)  $( - 8,8 )$ 
A)  $( 8 , \infty )$ 
B)  $( - \infty , - 8 ) \cup ( 8 , \infty )$ 
C)  $( - \infty , - 8 )$ 
D)  $( - 8,8 )$

Question 11

Solve the problem. Round your answer to three decimals.
-How long will it take for an investment to double in value if it earns 9.25% compounded continuously?

Accepted Answer

A)  7.493 years 
B)  3.747 years 
C)  7.781 years 
D)  11.877 years 
A)  7.493 years 
B)  3.747 years 
C)  7.781 years 
D)  11.877 years

Question 12

Write as the sum and/or difference of logarithms. Express powers as factors.
-$\log _ { 7 } \frac { \sqrt [ 2 ] { 15 } } { y ^ { 2 } x }$

Accepted Answer

A)  $\frac { 1 } { 2 } \log _ { 7 } 15 - 2 \log _ { 7 } y - 2 \log _ { 7 } x$ 
B)  $\frac { 1 } { 2 } \log _ { 7 } 15 - 2 \log _ { 7 } y - \log _ { 7 } x$ 
C)  $\log _ { 19 } 5 - \log _ { 19 } n - \log _ { 19 } m$ 
D)  $2 \log _ { 7 } 15 - 2 \log _ { 7 } y - \log _ { 7 } 2$ 
A)  $\frac { 1 } { 2 } \log _ { 7 } 15 - 2 \log _ { 7 } y - 2 \log _ { 7 } x$ 
B)  $\frac { 1 } { 2 } \log _ { 7 } 15 - 2 \log _ { 7 } y - \log _ { 7 } x$ 
C)  $\log _ { 19 } 5 - \log _ { 19 } n - \log _ { 19 } m$ 
D)  $2 \log _ { 7 } 15 - 2 \log _ { 7 } y - \log _ { 7 } 2$

Question 13

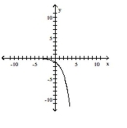
The graph of an exponential function is given. Match the graph to one of the following functions.
-

Accepted Answer

A)  $f ( x ) = 2 ^ { - x }$ 
B)  $f ( x ) = - 2 ^ { - x }$ 
C)  $f ( x ) = 2 ^ { x }$ 
D)  $f ( x ) = - 2 ^ { x }$ 
A)  $f ( x ) = 2 ^ { - x }$ 
B)  $f ( x ) = - 2 ^ { - x }$ 
C)  $f ( x ) = 2 ^ { x }$ 
D)  $f ( x ) = - 2 ^ { x }$

Question 14

Use the properties of logarithms to find the exact value of the expression. Do not use a calculator.
-$\log _ { 4 } 21 \cdot \log _ { 21 } 64$

Accepted Answer

A)  21 
B)  4 
C)  64 
D)  3 
A)  21 
B)  4 
C)  64 
D)  3

Question 15

Use the Change-of-Base Formula and a calculator to evaluate the logarithm. Round your answer to three decimal places.
-$\log _ { 4.4 } 2.6$

Accepted Answer

A)  $0.645$ 
B)  $0.591$ 
C)  $1.551$ 
D)  $0.415$ 
A)  $0.645$ 
B)  $0.591$ 
C)  $1.551$ 
D)  $0.415$

Question 16

Solve the equation.
-$243 ^ { 3 x - 1 } = 27 ^ { 2 x }$

Accepted Answer

A)  $\left\{ \frac { 9 } { 5 } \right\}$ 
B)  $\left\{ - \frac { 9 } { 5 } \right\}$ 
C)  $\left\{ \frac { 5 } { 9 } \right\}$ 
D)  $\left\{ - \frac { 5 } { 9 } \right\}$ 
A)  $\left\{ \frac { 9 } { 5 } \right\}$ 
B)  $\left\{ - \frac { 9 } { 5 } \right\}$ 
C)  $\left\{ \frac { 5 } { 9 } \right\}$ 
D)  $\left\{ - \frac { 5 } { 9 } \right\}$

Question 17

Choose the one alternative that best completes the statement or answers the question.
-The logistic growth model $\mathrm { P } ( \mathrm { t } ) = \frac { 900 } { 1 + 21.5 \mathrm { e } ^ { - 0.352 \mathrm { t } } }$ represents the population of a bacterium in a culture tube after $t$ hours. When will the amount of bacteria be 760 ?

Accepted Answer

A)  $7.84$ hours 
B)  $2.55$ hours 
C)  $8.24$ hours 
D)  $13.52$ hours 
A)  $7.84$ hours 
B)  $2.55$ hours 
C)  $8.24$ hours 
D)  $13.52$ hours

Question 18

Choose the one alternative that best completes the statement or answers the question.
Solve the equation.
-$$8 + 5 \ln x = 16$$

Accepted Answer

A)  $\left\{ e ^ { 8 / 5 } \right\}$ 
B)  $\left\{ \frac { 8 } { 5 \ln 1 } \right\}$ 
C)  $\left\{ \frac { e ^ { 8 } } { 5 } \right\}$ 
D)  $\left\{ \ln \left( \frac { 8 } { 5 } \right) \right\}$ 
A)  $\left\{ e ^ { 8 / 5 } \right\}$ 
B)  $\left\{ \frac { 8 } { 5 \ln 1 } \right\}$ 
C)  $\left\{ \frac { e ^ { 8 } } { 5 } \right\}$ 
D)  $\left\{ \ln \left( \frac { 8 } { 5 } \right) \right\}$

Question 19

Solve the problem.
-Find the amount in a savings account at the end of 7 years if the amount originally deposited is $3,000 and the interest rate is 5.5% compounded quarterly. Use: $A = P \left( 1 + \frac { r } { n } \right) ^ { n t }$ where:
$\mathrm { A } =$ final amount
$\mathrm { P } = \$ 3,000$ (the initial deposit)
$\mathrm { r } = 5.5 \% = 0.055$ (the annual rate of interest)
$\mathrm { n } = 4$ (the number of times interest is compounded each year)
$t = 7$ (the duration of the deposit in years)

Accepted Answer

A)  $\$ 85,155.00$ 
B)  $\$ 4,397.29$ 
C)  $\$ 3,300.94$ 
D)  $\$ 4,837.02$ 
A)  $\$ 85,155.00$ 
B)  $\$ 4,397.29$ 
C)  $\$ 3,300.94$ 
D)  $\$ 4,837.02$

Question 20

Choose the one alternative that best completes the statement or answers the question.
-The logistic growth function $\mathrm { f } ( \mathrm { t } ) = \frac { 24,000 } { 1 + 599.0 \mathrm { e } ^ { - 1.8 \mathrm { t } } }$ models the number of people who have become ill with a particular infection t weeks after its initial outbreak in a particular community. What is the limiting size of the population that becomes ill?

Accepted Answer

A)  599 people 
B)  24,000 people 
C)  600 people 
D)  48,000 people 
A)  599 people 
B)  24,000 people 
C)  600 people 
D)  48,000 people

Find the domain of the function. - $f ( x ) = \ln \sqrt { x }$

Decide whether or not the functions are inverses of each other. - $f ( x ) = 9 x - 9 , g ( x ) = \frac { 1 } { 9 } x + 1$

Solve the problem. -Suppose that $f ( x ) = 3 ^ { x }$ . If $f ( x ) = \frac { 1 } { 729 }$ , what is $x$ ?

Choose the one alternative that best completes the statement or answers the question. Solve the exponential equation. Use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. - $4 ^ { x + 7 } = 7$

Decide whether or not the functions are inverses of each other. - $f ( x ) = ( x - 6 ) ^ { 2 } , x \geq 6 ; \quad g ( x ) = \sqrt { x + 6 }$

Use a graphing calculator to solve the equation. Round your answer to two decimal places. - $e ^ { x } = x ^ { 3 }$

Choose the one alternative that best completes the statement or answers the question. -If Emery has $1,100 to invest at 9% per year compounded monthly, how long will it be before he has $1,400? If the compounding is continuous, how long will it be? (Round your answers to three decimal places.)

Find the exact value of the logarithmic expression. - $\ln \mathrm { e }$

Find the domain of the function. - $f ( x ) = \log _ { 10 } \left( \frac { x + 8 } { x - 8 } \right)$

Solve the problem. Round your answer to three decimals. -How long will it take for an investment to double in value if it earns 9.25% compounded continuously?

Write as the sum and/or difference of logarithms. Express powers as factors. - $\log _ { 7 } \frac { \sqrt [ 2 ] { 15 } } { y ^ { 2 } x }$

The graph of an exponential function is given. Match the graph to one of the following functions. -

Use the properties of logarithms to find the exact value of the expression. Do not use a calculator. - $\log _ { 4 } 21 \cdot \log _ { 21 } 64$

Use the Change-of-Base Formula and a calculator to evaluate the logarithm. Round your answer to three decimal places. - $\log _ { 4.4 } 2.6$

Solve the equation. - $243 ^ { 3 x - 1 } = 27 ^ { 2 x }$

Choose the one alternative that best completes the statement or answers the question. Solve the equation. - $8 + 5 \ln x = 16$

Functions and Their Graphs

Linear and Quadratic Functions

Polynomial and Rational Functions

Trigonometric Functions

Analytic Trigonometry

Applications of Trigonometric Functions

Polar Coordinates; Vectors

Analytic Geometry

Systems of Equations and Inequalities

Sequences; Induction; the Binomial Theorem

Counting and Probability

A Preview of Calculus: the Limit, Derivative, and Integral of a Function

Foundations: a Prelude to Functions

Graphing Utilities

Filters

Exam 4: Exponential and Logarithmic Functions

Find the domain of the function. - f(x)=ln⁡xf ( x ) = \ln \sqrt { x }f(x)=lnx​

Decide whether or not the functions are inverses of each other. - f(x)=9x−9,g(x)=19x+1f ( x ) = 9 x - 9 , g ( x ) = \frac { 1 } { 9 } x + 1f(x)=9x−9,g(x)=91​x+1

Solve the problem. -Suppose that f(x)=3xf ( x ) = 3 ^ { x }f(x)=3x . If f(x)=1729f ( x ) = \frac { 1 } { 729 }f(x)=7291​ , what is xxx ?

Choose the one alternative that best completes the statement or answers the question. Solve the exponential equation. Use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. - 4x+7=74 ^ { x + 7 } = 74x+7=7

Decide whether or not the functions are inverses of each other. - f(x)=(x−6)2,x≥6;g(x)=x+6f ( x ) = ( x - 6 ) ^ { 2 } , x \geq 6 ; \quad g ( x ) = \sqrt { x + 6 }f(x)=(x−6)2,x≥6;g(x)=x+6​

Use a graphing calculator to solve the equation. Round your answer to two decimal places. - ex=x3e ^ { x } = x ^ { 3 }ex=x3