Exam 10: Systems of Equations and Inequalities

Choose the one alternative that best completes the statement or answers the question. Solve the problem. -The liquid portion of a diet is to provide at least 300 calories, 36 units of vitamin $A$ , and 90 units of vitamin $C$ daily. A cup of dietary drink $X$ provides 60 calories, 12 units of vitamin $A$ , and 10 units of vitamin C. A cup of dietary drink $Y$ provides 60 calories, 6 units of vitamin $A$ , and 30 units of vitamin $C$ . Set up a system of linear inequalities that describes the minimum daily requirements for calories and vitamins. Let $x =$ number of cups of dietary drink $X$ , and $y =$ number of cups of dietary drink $Y$ . Write all the constraints as a system of linear inequalities.

Choose the one alternative that best completes the statement or answers the question. Find the value of the determinant. - $\left| \begin{array} { l l } 6 & 3 \\5 & 2\end{array} \right|$

Solve the system of equations. - $\left\{ \begin{array} { r } x + 4 y - z = 3 \\x + 5 y - 2 z = 5 \\3 x + 12 y - 3 z = 9\end{array} \right.$

Write the word or phrase that best completes each statement or answers the question. Solve for x. - $\left| \begin{array} { r r r } x & - 4 & - 1 \\- 2 & 2 & 0 \\- 1 & - 2 & 8\end{array} \right| = 10$

Solve the problem. -An 8-cylinder Crown Victoria gives 18 miles per gallon in city driving and 21 miles per gallon in highway driving. A 300-mile trip required 15.5 gallons of gasoline. How many whole miles were driven in the city?

Perform the indicated matrix operations. -Let $A = \left[ \begin{array} { l l } - 4 & 2 \end{array} \right]$ and $B = \left[ \begin{array} { l l } 1 & 0 \end{array} \right]$ . Find $3 A + 4 B$ .

Use the properties of determinants to find the value of the second determinant, given the value of the first. - $\left| \begin{array} { c c c } x & y & z \\u & v & w \\1 & - 1 & 3\end{array} \right| = - 51 \left| \begin{array} { c c c } 1 & - 1 & 3 \\2 u & 2 v & 2 w \\x - 1 & y + 1 & z - 3\end{array} \right| = ?$

Write the partial fraction decomposition of the rational expression. - $\frac { - 4 x ^ { 2 } - 6 x + 2 } { ( x + 2 ) ( x + 1 ) ^ { 2 } }$

Choose the one alternative that best completes the statement or answers the question. -A doctor has told a patient to take vitamin pills. The patient needs at least 28 units of vitamin A, at least 8 units of vitamin C, and at least 76 units of vitamin D. The red vitamin pills cost 20¢ each and contain 8 units of A, 1 Unit of C, and 7 units of D. The blue vitamin pills cost 40¢ each and contain 3 units of A, 1 unit of C, and 11 units Of D. How many pills should the patient take each day to minimize costs?

Write the word or phrase that best completes each statement or answers the question. -The difference of two numbers is 5 and the difference of their squares is 55. Find the numbers.

Solve the system of equations by using substitution. - $\left\{ \begin{array} { r } 5 x - 2 y = - 1 \\x + 4 y = 35\end{array} \right.$

Solve the problem. -A movie theater charges $8.00 for adults and $5.00 for children. If there were 40 people altogether and the theater collected $272.00 at the end of the day, how many of them were adults?

Choose the one alternative that best completes the statement or answers the question. Use Cramer's rule to solve the linear system. - $\left\{ \begin{array} { l } 3 x + 3 y = 51 \\2 x - 2 y = 2 \\\end{array} \right.$

The graph of two equations along with the points of intersection are given. Substitute the points of intersection into the systems of equations. Are the points of intersection solutions to the system of equations (Y/N)? -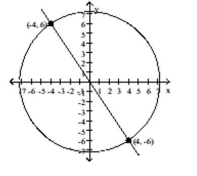 +=52 2y+3x=0

Solve the system of equations. - $\left\{ \begin{aligned}x - y + 4 z & = 2 \\5 x + z & = 0 \\x + 2 y + z & = - 4\end{aligned} \right.$

Write the word or phrase that best completes each statement or answers the question. Which method should be used to solve the system? Explain your answer, including a description of the first step. - -=36 3x-y=-6

Write the word or phrase that best completes each statement or answers the question. Which method should be used to solve the system? Explain your answer, including a description of the first step. - 9+3 =81 -8-10 =9

Verify that the values of the variables listed are solutions of the system of equations. - $\left\{ \begin{array} { c } x + y + z = 6 \\x - y + 4 z = 14 \\5 x + y + z = 26 \\\end{array} \right.$ x = 5 , y = - 1 , z = 2

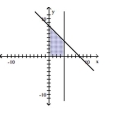
Write a system of linear inequalities that has the given graph. -

Solve the system using the inverse method. - $\left\{ \begin{array} { r } x + 2 y + 3 z = - 8 \\x + y + z = - 4 \\- x + y + 2 z = - 1\end{array} \right.$