Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs297 Questions
Exam 2: Linear and Quadratic Functions302 Questions
Exam 3: Polynomial and Rational Functions354 Questions
Exam 4: Exponential and Logarithmic Functions517 Questions
Exam 5: Trigonometric Functions354 Questions
Exam 6: Analytic Trigonometry342 Questions
Exam 7: Applications of Trigonometric Functions105 Questions
Exam 8: Polar Coordinates; Vectors253 Questions
Exam 9: Analytic Geometry200 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability115 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Foundations: a Prelude to Functions234 Questions
Exam 15: Graphing Utilities29 Questions
Select questions type
Solve.
-The amount of water used to take a shower is directly proportional to the amount of time that the shower is in use. A shower lasting 17 minutes requires 10.2 gallons of water. Find the amount of water used in a shower
Lasting 12 minutes.
(Multiple Choice)
4.9/5  (39)
(39)
Find an equation of the secant line containing (1, f(1)) and (2, f(2)).
-
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-Sue wants to put a rectangular garden on her property using 76 meters of fencing. There is a river that runs through her property so she decides to increase the size of the garden by using the river as one side of the rectangle. (Fencing is then needed only on the other three sides.) Let x represent the length of the side of the rectangle along the river. Express the garden's area as a function of .
(Multiple Choice)
4.7/5  (34)
(34)
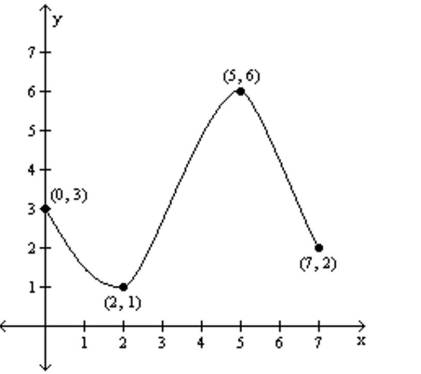
For the graph of the function y = f(x), find the absolute maximum and the absolute minimum, if it exists.
-
(Multiple Choice)
4.9/5  (39)
(39)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
(Multiple Choice)
4.7/5  (24)
(24)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-The gravitational attraction A between two masses varies inversely as the square of the distance between them. The force of attraction is 9 lb when the masses are 2 ft apart, what is the attraction when the masses are 6 ft
Apart?
(Multiple Choice)
4.9/5  (30)
(30)
Choose the one alternative that best completes the statement or answers the question.
-The concentration (arbitrary units) of a certain drug in a patient's bloodstream can be modeled using , where is the number of hours since a 500 milligram oral dose was administered. Using the TABLE feature of a graphing utility, find the time at which the concentration of the drug is greatest. Round to the nearest tenth of an hour.
(Multiple Choice)
4.9/5  (37)
(37)
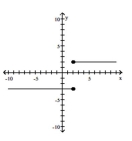
Determine whether the graph is that of a function. If it is, use the graph to find its domain and range, the intercepts, if
any, and any symmetry with respect to the x-axis, the y-axis, or the origin.
-
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-Express the gross salary of a person who earns per hour as a function of the number of hours worked.
(Multiple Choice)
4.8/5  (46)
(46)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.8/5  (26)
(26)
Solve the problem.
-A wire of length is bent into the shape of a square. Express the area A of the square as a function of x.
(Multiple Choice)
4.9/5  (40)
(40)
For the given functions f and g, find the requested function and state its domain.
-
Find .
(Multiple Choice)
5.0/5  (38)
(38)
If y varies directly as x, find a linear function which relates them.
-
(Multiple Choice)
4.9/5  (27)
(27)
Solve.
-The amount of gas that a helicopter uses is directly proportional to the number of hours spent flying. The helicopter flies for 2 hours and uses 18 gallons of fuel. Find the number of gallons of fuel that the helicopter uses
To fly for 5 hours.
(Multiple Choice)
4.9/5  (30)
(30)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-
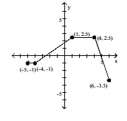
(Multiple Choice)
4.9/5  (39)
(39)
Showing 181 - 200 of 297
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)