Exam 1: Review of Basic Concepts
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Decide whether the expression has been simplified correctly.
-
(Multiple Choice)
4.8/5  (35)
(35)
Write the expression with only positive exponents and evaluate if possible. Assume all variables represent nonzero real
numbers.
-
(Multiple Choice)
4.8/5  (33)
(33)
Simplify the rational expression. Use factoring, and assume all variable expressions represent positive real numbers.
-A manufacturer's cost is given b , where C is the cost in dollars and n is the number of parts produced. Find the cost when 216 parts are produced.
(Multiple Choice)
4.8/5  (30)
(30)
Simplify the expression. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.7/5  (40)
(40)
Simplify the rational expression. Use factoring, and assume all variable expressions represent positive real numbers.
-If the lengths of the sides of a square are tripled, by what factor will the area change?
(Multiple Choice)
4.7/5  (29)
(29)
Rationalize the denominator. Assume that all variables represent nonnegative numbers and that the denominator is not
zero.
-
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem. Round to two decimal places unless otherwise indicated.
-In the following formula, is the minimum number of hours of studying required to attain a test score of : . How many hours of study are needed to score
(Multiple Choice)
4.9/5  (33)
(33)
Write the expression with only positive exponents and evaluate if possible. Assume all variables represent nonzero real numbers.
-
(Multiple Choice)
4.8/5  (26)
(26)
Perform the indicated operations. Write the result using only positive exponents. Assume all variables represent nonzero
real numbers.
-
(Multiple Choice)
4.8/5  (37)
(37)
Simplify the expression. Assume all variables represent positive real numbers.
-
(Multiple Choice)
4.9/5  (41)
(41)
Provide an appropriate response.
-Consider the following figure, which is a square divided into two squares and two rectangles.
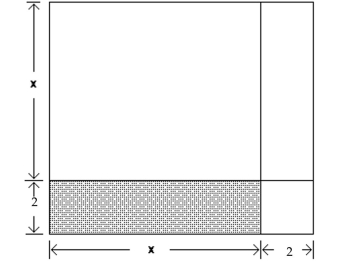 The length of each side of the large square is , which means that the area of the largest square is . Use the formulas for the area of a square and the area of a rectangle to write the area of the largest square as a trinomial that represents the sum of the areas of the four figures that comprise it.
The length of each side of the large square is , which means that the area of the largest square is . Use the formulas for the area of a square and the area of a rectangle to write the area of the largest square as a trinomial that represents the sum of the areas of the four figures that comprise it.
(Multiple Choice)
4.9/5  (33)
(33)
Showing 61 - 80 of 637
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)