Exam 9: Systems and Matrices
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Solve the problem using matrices.
-A chemist has prepared two acid solutions, one of which is acid by volume, another acid. How many cubic centimeters of each should the chemist mix together to obtain of a solution that is acid.
(Multiple Choice)
4.9/5  (39)
(39)
Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, let the last
variable be the arbitrary variable.
- 3x-y+3z=28 7x+4z=65 8y+z=44
(Multiple Choice)
4.9/5  (33)
(33)
Write the augmented matrix for the system. Do not solve the system.
- -2x+3y+3z=37 6x+4y+3z=27 7x-2y-2z=-36
(Multiple Choice)
4.8/5  (32)
(32)
Give all solutions of the nonlinear system of equations, including those with nonreal complex components.
- 5+3xy-5=-9 -xy-=-5
(Multiple Choice)
4.8/5  (48)
(48)
A nonlinear system is given, along with the graphs of both equations in the system. Determine if the points of
intersection specified on the graph are solutions of the system by substituting directly into both equations.
- =y-1 y=2x+16
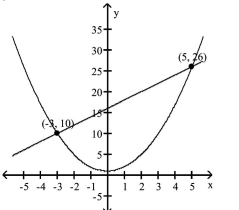
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-A bookstore is having a sale. All books included in the sale have a colored sticker on them to indicate the sale price. There are green stickers, red stickers, and orange stickers. Bob, Sue, and Fred each make purchases of books that are on sale. Each row of the table gives information about the numbers of book purchases and the total cost of the purchase (before taxes).
![Solve the problem. -A bookstore is having a sale. All books included in the sale have a colored sticker on them to indicate the sale price. There are green stickers, red stickers, and orange stickers. Bob, Sue, and Fred each make purchases of books that are on sale. Each row of the table gives information about the numbers of book purchases and the total cost of the purchase (before taxes). Use this information to set up a matrix equation of the form A X = B , which can be solved to determine the price for each type of sale book. Solve this matrix equation to find the price of a book with an orange sticker. Use the fact that for A = \left[ \begin{array} { l l l } 1 & 2 & 2 \\ 1 & 3 & 2 \\ 1 & 2 & 3 \end{array} \right] , A ^ { - 1 } = \left[ \begin{array} { r r r } 5 & - 2 & - 2 \\ - 1 & 1 & 0 \\ - 1 & 0 & 1 \end{array} \right] .](https://storage.examlex.com/TB4654/11eccc69_e0e1_a840_bd49_13f513b26b95_TB4654_11.jpg) Use this information to set up a matrix equation of the form , which can be solved to determine the price for each type of sale book. Solve this matrix equation to find the price of a book with an orange sticker.
Use the fact that for .
Use this information to set up a matrix equation of the form , which can be solved to determine the price for each type of sale book. Solve this matrix equation to find the price of a book with an orange sticker.
Use the fact that for .
(Multiple Choice)
4.9/5  (32)
(32)
Solve the system in terms of the arbitrary variable x.
- x+y+z=9 4x-3y+2z=7
(Multiple Choice)
4.8/5  (43)
(43)
Solve the problem.
-Matt bought 3 pounds of oranges and 2 pounds of apples and paid , before tax. Andy bought 4 pounds of oranges and 3 pounds of apples and paid , before tax. Use this information to set up a matrix equation of the form , which can be solved to determine the price per pound for oranges and apples. Solve this matrix equation to find the price per pound of apples.
Use the fact that for .
(Multiple Choice)
4.8/5  (40)
(40)
Solve the system by using the inverse of the coefficient matrix.
- 2x+8y+6z=20 4x+2y-2z=-2 3x-y+z=11
(Multiple Choice)
4.7/5  (35)
(35)
Solve each problem.
-Le Boulangerie, a bakery, sells four main items: sweet rolls, bread, cakes, and pies. The amount of each ingredient (in cups, except for eggs) required for these items is given by matrix A.
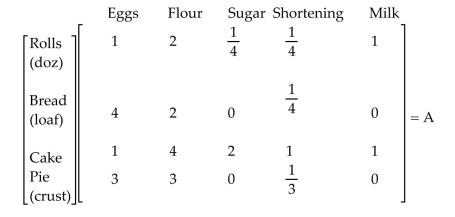 Suppose a day's orders consist of 20 dozen sweet rolls, 200 loaves of bread, 50 cakes, and 60 pies. Write the orders as a matrix and, using matrix multiplication, write as a matrix the amount of each ingredient needed to fill the day's orders.
Suppose a day's orders consist of 20 dozen sweet rolls, 200 loaves of bread, 50 cakes, and 60 pies. Write the orders as a matrix and, using matrix multiplication, write as a matrix the amount of each ingredient needed to fill the day's orders.
(Multiple Choice)
4.8/5  (36)
(36)
Solve each problem.
-Le Boulangerie, a bakery, sells four main items: sweet rolls, bread, cakes, and pies. The amount of each ingredient (in cups, except for eggs) required for these items is given by matrix A.
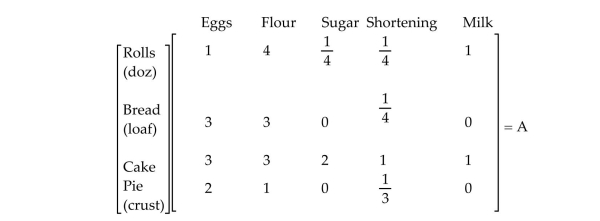 The cost (in cents) for each ingredient when purchased in large lots or small lots is given in matrix B.
The cost (in cents) for each ingredient when purchased in large lots or small lots is given in matrix B.
 Suppose a day's orders consist of 20 dozen sweet rolls, 200 loaves of bread, 50 cakes, and 60 pies. Use matrix multiplication to find a matrix giving the costs under the two purchase options to fill the day's orders.
Suppose a day's orders consist of 20 dozen sweet rolls, 200 loaves of bread, 50 cakes, and 60 pies. Use matrix multiplication to find a matrix giving the costs under the two purchase options to fill the day's orders.
(Multiple Choice)
4.8/5  (44)
(44)
Write the word or phrase that best completes each statement or answers the question.
Provide an appropriate response.
-Let be a matrix that has a multiplicative inverse. Which of the following statements are false? (Let 0 represent the zero matrix.)
(i)
(ii)
(iii)
(iv)
(Multiple Choice)
4.9/5  (38)
(38)
Solve the system by using the inverse of the coefficient matrix.
- 3x+5y=-10 2x+4y=-6
(Multiple Choice)
4.7/5  (31)
(31)
Provide an appropriate response.
-5x + 3y = 19
7x + 8y = 48
If your friend were going to solve this system of equations by first eliminating y, what
general suggestions would you make so your friend could start on this in a systematic
way?
(Essay)
4.8/5  (45)
(45)
Use a graphing calculator and the method of matrix inverses to solve the system. Give five decimal places, if necessary.
- 3.2x+\piy= x-7.84y=4
(Multiple Choice)
4.7/5  (41)
(41)
Showing 341 - 360 of 505
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)