Exam 9: Systems and Matrices
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Graph the solution set of the system of inequalities.
- y-x\leq5 x+y\geq3 y-3x\geq-1
(Multiple Choice)
4.9/5  (41)
(41)
Use Cramerʹs rule to solve the system of equations. If D = 0, use another method to determine the solution set.
- -7x+92=9y -2x-6y=-40
(Multiple Choice)
4.7/5  (45)
(45)
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.
- 3x+2y+z=4 2x-3y-z=5 5x+12y+5z=2
(Multiple Choice)
4.7/5  (35)
(35)
Solve the system by using the inverse of the coefficient matrix.
- -3x+y+3z-w=-1 -x-4y+z-2w=-15 -4x+3y-3z+w=20 3x-y-z-2w=-6
(Multiple Choice)
4.7/5  (40)
(40)
Decide whether or not the matrices are inverses of each other.
- and
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-The perimeter of a rectangle is 38 m. If the width were doubled and the length were increased by 10 m, the perimeter would be 70 m. What are the length and width of the rectangle?
(Multiple Choice)
4.9/5  (31)
(31)
Graph the solution set of the system of inequalities.
- +\leq1 +\leq1
(Multiple Choice)
4.7/5  (34)
(34)
Provide an appropriate response.
-Fill in the blanks to complete the statement. For a system of 2 equations and 2 unknowns, the corresponding augmented matrix will have _______ rows and _______ columns.
(Multiple Choice)
4.7/5  (42)
(42)
Provide an appropriate response.
-Fill in the blank to complete the statement. Each number in a matrix is called _______ of the matrix.
(Multiple Choice)
4.8/5  (34)
(34)
Solve the system for x and y using Cramerʹs rule. Assume a and b are nonzero constants.
- x+by= x+ay=
(Multiple Choice)
4.7/5  (36)
(36)
Use Cramerʹs rule to solve the system of equations. If D = 0, use another method to determine the solution set.
- x+y+z=-1 x-y+3z=7 3x+y+z=-3
(Multiple Choice)
4.7/5  (40)
(40)
Use the shading capabilities of your graphing calculator to graph the inequality or system of inequalities.
- y\leq3 y\geq
(Multiple Choice)
4.8/5  (31)
(31)
Decide whether or not the matrices are inverses of each other.
- and
(Multiple Choice)
4.9/5  (34)
(34)
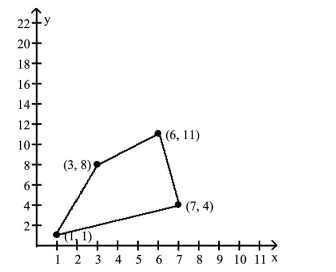
The graph shows the region of feasible solutions. Find the maximum or minimum value, as specified, of the objective
function.
-objective function ; minimum
(Multiple Choice)
4.8/5  (37)
(37)
Showing 421 - 440 of 505
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)