Exam 3: Polynomial and Rational Functions
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Find a polynomial of degree 3 with real coefficients that satisfies the given conditions.
-Zero of having multiplicity 2 and zero of 10 having multiplicity
(Multiple Choice)
4.8/5  (43)
(43)
Solve the problem.
-A rock is propelled upward from the top of a building 160 feet tall at an initial velocity of 48 feet per second. The function that describes the height of the rocket in terms of time is . Determine the maximum height that the rock reaches.
(Multiple Choice)
4.9/5  (37)
(37)
Use the graph to answer the question.
-Find the domain of the rational function graphed below.
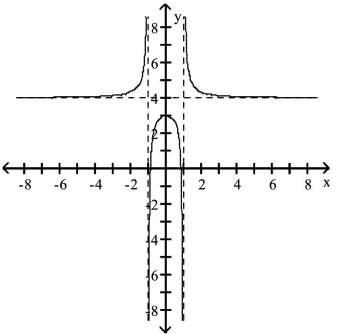
(Multiple Choice)
4.8/5  (31)
(31)
Find the equation of the axis of symmetry of the parabola.
-
(Multiple Choice)
4.8/5  (42)
(42)
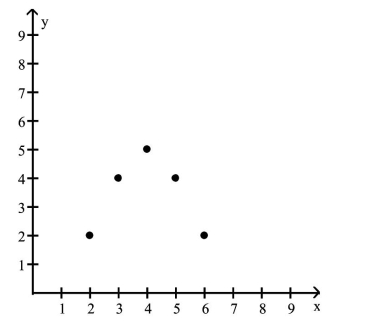
Tell whether a linear model or a quadratic model is appropriate for the data. If linear, tell whether the slope
positive or negative. If quadratic, decide whether the leading coefficient a of x2 should be positive or negative.
-
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem. Round your answer to two decimal places.
-The weight W of an object on the Moon varies directly as the weight E on earth. A person who weighs 114 lb on earth weighs 22.8 lb on the Moon. How much would a 180-lb person weigh on
The Moon?
(Multiple Choice)
4.9/5  (32)
(32)
Factor f(x) into linear factors given that k is a zero of f(x).
- (multiplicity 2)
(Multiple Choice)
4.8/5  (29)
(29)
Use the intermediate value theorem for polynomials to show that the polynomial function has a real zero between the
numbers given.
-
(Multiple Choice)
4.7/5  (37)
(37)
Solve the problem.
-Bob owns a watch repair shop. He has found that the cost of operating his shop is given by , where is cost and is the number of watches repaired. How many watches must he repair to have the lowest cost?
(Multiple Choice)
4.8/5  (33)
(33)
Use a graphing calculator to approximate the real zeros. Give each zero as a decimal to the nearest tenth.
-
(Multiple Choice)
4.9/5  (33)
(33)
Use the intermediate value theorem for polynomials to show that the polynomial function has a real zero between the
numbers given.
- and 2
(Multiple Choice)
4.9/5  (27)
(27)
Solve the problem.
-The pitch of a musical tone varies inversely as its wavelength . One tone has a pitch of 202 vibrations per second and a wavelength of . Find the wavelength of another tone that a pitch of 481 vibrations per second. Round to the nearest tenth.
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-The height of a box is 8 inches. The length is three inches more than the width. Find the width if the volume is 864 cubic inches.
(Multiple Choice)
4.9/5  (46)
(46)
Use the equation and the corresponding graph for the quadratic function to find what is requested.
-
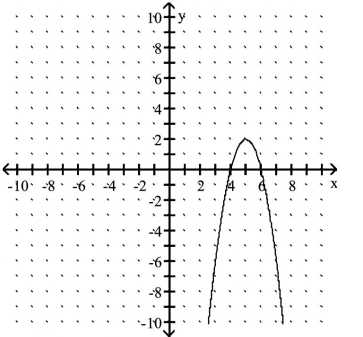 Find the -intercepts.
Find the -intercepts.
(Multiple Choice)
4.8/5  (45)
(45)
Use synthetic division to decide whether the given number k is a zero of the given polynomial function.
-
(Multiple Choice)
4.7/5  (29)
(29)
Use the remainder theorem and synthetic division to find f(k).
-
(Multiple Choice)
4.8/5  (35)
(35)
Find the zeros of the polynomial function and state the multiplicity of each.
-
(Multiple Choice)
4.7/5  (44)
(44)
Answer the question
-If y varies inversely as x, and x is halved, how is y changed?
(Multiple Choice)
4.8/5  (33)
(33)
Showing 361 - 380 of 516
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)