Exam 3: Polynomial and Rational Functions
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Translate the given formula to an English phrase using the word ʺvariesʺ.
- stop , where stop is camera setting with a lens with focal length and diaphragm opening D
(Essay)
4.8/5  (43)
(43)
Express f(x) in the form f(x) = (x - k)q(x) + r for the given value of k.
-
(Multiple Choice)
4.8/5  (44)
(44)
Graph the polynomial function. Factor first if the expression is not in factored form.
-
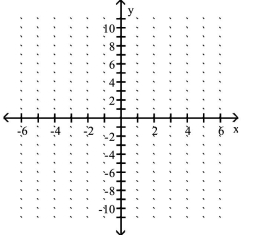
(Multiple Choice)
4.7/5  (31)
(31)
Solve the problem.
-The number of mosquitoes , in millions, in a certain area depends on the June rainfall , in inches: . What rainfall produces the maximum number of mosquitoes?
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-The length of a rectangle is 4 inches more than its width. If 2 inches are taken from the length and added to the width, the figure becomes a square with an area of 144 square inches. What are the dimensions of the original figure?
(Multiple Choice)
4.7/5  (31)
(31)
Translate the given formula to an English phrase using the word ʺvariesʺ.
-
(Short Answer)
4.9/5  (35)
(35)
Find the correct end behavior diagram for the given polynomial function.
-
(Multiple Choice)
5.0/5  (32)
(32)
Find a polynomial of least degree with only real coefficients and having the given zeros.
- , and 1 (multiplicity 2 )
(Multiple Choice)
4.8/5  (32)
(32)
Use synthetic division to decide whether the given number k is a zero of the given polynomial function.
-
(Multiple Choice)
4.8/5  (40)
(40)
Find the zeros of the polynomial function and state the multiplicity of each.
-
(Multiple Choice)
4.9/5  (39)
(39)
Give all possible rational zeros for the following polynomial.
-
(Multiple Choice)
4.9/5  (35)
(35)
Factor f(x) into linear factors given that k is a zero of f(x).
- (multiplicity 2
(Multiple Choice)
4.8/5  (40)
(40)
Use a graphing calculator to find the coordinates of the turning points of the graph of the polynomial function in the
indicated domain interval. Give answers to the nearest hundredth.
-
(Multiple Choice)
4.9/5  (37)
(37)
Determine whether the statement is true or false.
-If f(x) is a polynomial having only real coefficients and 2 - 4i is a zero of f(x), then 2 + 4i is also a
zero.
(True/False)
4.9/5  (37)
(37)
Use the remainder theorem and synthetic division to find f(k).
-
(Multiple Choice)
4.9/5  (36)
(36)
Answer the question
-How can the graph of be obtained from the graph of ?
(Multiple Choice)
4.9/5  (39)
(39)
Solve the problem. Round to the nearest tenth unless indicated otherwise.
-Wind resistance or atmospheric drag tends to slow down moving objects. Atmospheric drag varies jointly as an object's surface area A and velocity v. If a car traveling at a speed of with a surface area of experiences a drag of (Newtons), how fast must a car with of surface area travel in order to experience a drag force of ?
(Multiple Choice)
4.9/5  (38)
(38)
Determine whether the statement is true or false.
-If f(x) is a polynomial and f(-5) = 0, then x + 5 is a factor of f(x).
(True/False)
4.9/5  (42)
(42)
Solve the problem.
-If varies directly as and inversely as , and when and , find when and
(Multiple Choice)
5.0/5  (40)
(40)
Showing 301 - 320 of 516
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)