Exam 3: Polynomial and Rational Functions
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Answer the question
-Suppose z varies directly as the square of x and inversely as y. If x is halved and y is tripled, what happens to z?
(Multiple Choice)
4.7/5  (45)
(45)
Find a polynomial of degree 3 with real coefficients that satisfies the given conditions.
-Zeros of and
(Multiple Choice)
4.9/5  (41)
(41)
Use the equation and the corresponding graph for the quadratic function to find what is requested.
-
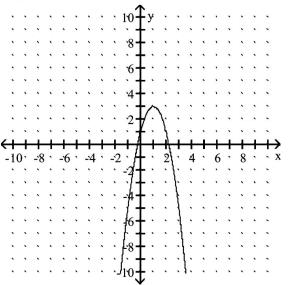 Find the domain and range.
Find the domain and range.
(Multiple Choice)
4.9/5  (32)
(32)
Factor f(x) into linear factors given that k is a zero of f(x).
-
(Multiple Choice)
4.7/5  (37)
(37)
Use a graphing calculator to find the coordinates of the turning points of the graph of the polynomial function in the
indicated domain interval. Give answers to the nearest hundredth.
-
(Multiple Choice)
4.9/5  (33)
(33)
Provide an appropriate response.
-Explain the behavior of the graph of as it approaches its vertical asymptote.
(Multiple Choice)
4.8/5  (42)
(42)
Find the correct end behavior diagram for the given polynomial function.
-
(Multiple Choice)
4.8/5  (26)
(26)
Translate the given formula to an English phrase using the word ʺvariesʺ.
- , where is the simple interest on a principal of dollars invested for years at an interest rate of per year
(Essay)
4.8/5  (32)
(32)
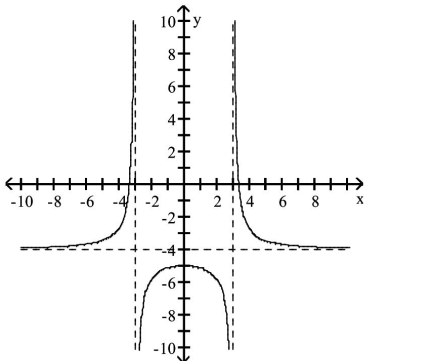
Identify any vertical, horizontal, or oblique asymptotes in the graph of y = f(x). State the domain of f.
-
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem. Round your answer to two decimal places.
-The distance to the horizon varies directly as the square root of the height above ground level of the observer. If a person can see 6 miles from a height of 25 feet, how far can a person see from a
Height of 49 feet?
(Multiple Choice)
4.7/5  (38)
(38)
Use a graphing calculator to approximate the real zeros. Give each zero as a decimal to the nearest tenth.
-
(Multiple Choice)
4.8/5  (29)
(29)
Use the graph to answer the question.
-Find the domain and range of the rational function graphed below.
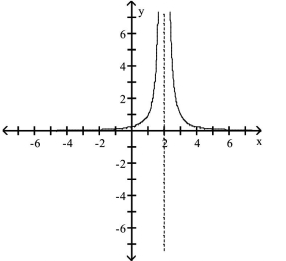
(Multiple Choice)
4.9/5  (38)
(38)
Give the domain and range for the rational function. Use interval notation.
-
(Multiple Choice)
4.8/5  (24)
(24)
Solve the problem.
-A coin is tossed upward from a balcony 242 feet high with an initial velocity of 16 feet per second, then its height after seconds is given by the equation . During what interval of time will the coin be at a height of at least ?
(Multiple Choice)
4.8/5  (36)
(36)
Translate the given formula to an English phrase using the word ʺvariesʺ.
-
(Essay)
4.9/5  (33)
(33)
Showing 441 - 460 of 516
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)