Exam 12: Exponential and Logarithmic Functions
Exam 1: Review of Real Numbers490 Questions
Exam 2: Equations, Inequalities, and Problem Solving332 Questions
Exam 3: Graphing313 Questions
Exam 4: Solving Systems of Linear Equations146 Questions
Exam 5: Exponents and Polynomials304 Questions
Exam 6: Factoring Polynomials261 Questions
Exam 7: Rational Expressions327 Questions
Exam 8: More on Functions and Graphs192 Questions
Exam 9: Inequalities and Absolute Value148 Questions
Exam 10: Rational Exponents, Radicals, and Complex Numbers379 Questions
Exam 11: Quadratic Equations and Functions242 Questions
Exam 12: Exponential and Logarithmic Functions302 Questions
Exam 13: Conic Sections153 Questions
Exam 14: Sequences, Series, and the Binomial Theorem201 Questions
Select questions type
Express as the logarithm of a single expression. Assume that variables represent positive numbers.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve.
-The size of the beaver population at a national park increases at the rate of per year. If the size of the current population is 101 , find how many beavers there should be in 6 years. Use and round to the nearest whole number.
(Multiple Choice)
4.9/5  (24)
(24)
Determine whether the function is a one-to-one function.
-
(Multiple Choice)
4.7/5  (39)
(39)
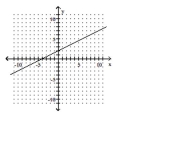
Graph the inverse of the function on the same set of axes.
-
(Multiple Choice)
4.8/5  (30)
(30)
Determine whether the function is one-to-one. If it is one-to-one find an equation or a set of ordered pairs that defines
the inverse function of the given function.
-
(Multiple Choice)
4.9/5  (42)
(42)
Write the expression as sums or differences of multiples of logarithms.
-
(Multiple Choice)
4.7/5  (38)
(38)
Solve the equation for x. Give an approximate solution accurate to four decimal places.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the equation for x. Give an approximate solution accurate to four decimal places.
-
(Multiple Choice)
4.8/5  (26)
(26)
Solve the logarithmic equation for x. Give an exact solution
-
(Multiple Choice)
4.8/5  (28)
(28)
The reliability of a new model of CD player can be described by the exponential function R(t) = 2.7-(1/3)t, where the
reliability R is the probability (as a decimal) that the CD player is still working t years after it is manufactured. Round the
answer to the nearest hundredth. Then write your answer as a percent.
-What is the probability that the CD player will still work 4 years after it is manufactured?
(Multiple Choice)
4.8/5  (34)
(34)
If the function is one-to-one, list the inverse function by switching coordinates or inputs and outputs.
-
(Multiple Choice)
4.9/5  (31)
(31)
Given the values of f and g, find the function value.
- Find .
(Multiple Choice)
4.9/5  (31)
(31)
Showing 261 - 280 of 302
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)