Exam 12: Exponential and Logarithmic Functions
Exam 1: Review of Real Numbers490 Questions
Exam 2: Equations, Inequalities, and Problem Solving332 Questions
Exam 3: Graphing313 Questions
Exam 4: Solving Systems of Linear Equations146 Questions
Exam 5: Exponents and Polynomials304 Questions
Exam 6: Factoring Polynomials261 Questions
Exam 7: Rational Expressions327 Questions
Exam 8: More on Functions and Graphs192 Questions
Exam 9: Inequalities and Absolute Value148 Questions
Exam 10: Rational Exponents, Radicals, and Complex Numbers379 Questions
Exam 11: Quadratic Equations and Functions242 Questions
Exam 12: Exponential and Logarithmic Functions302 Questions
Exam 13: Conic Sections153 Questions
Exam 14: Sequences, Series, and the Binomial Theorem201 Questions
Select questions type
Express as the logarithm of a single expression. Assume that variables represent positive numbers.
-
(Multiple Choice)
4.9/5  (36)
(36)
Graph the function and its inverse on the same set of axes.
-

(Multiple Choice)
4.7/5  (30)
(30)
Use a calculator to approximate the logarithm to four decimal places.
-
(Multiple Choice)
4.8/5  (39)
(39)
Solve.
-Find out how long it takes a investment to double if it is invested at compounded quarterly. Round to the nearest tenth of a year. Use the formula .
(Multiple Choice)
4.7/5  (32)
(32)
Use the properties of logarithms to write the expression as a single logarithm.
-
(Multiple Choice)
4.8/5  (39)
(39)
Write the expression as sums or differences of multiples of logarithms.
-
(Multiple Choice)
5.0/5  (34)
(34)
For the given functions f and g, find the composition.
- Find
(Multiple Choice)
4.9/5  (28)
(28)
Use the following approximations to find the approximate value of the logarithmic expression:
-
(Multiple Choice)
4.9/5  (28)
(28)
Graph the function and its inverse on the same set of axes.
-
(Multiple Choice)
4.8/5  (41)
(41)
Solve.
-The amount of a radioactive substance present, in grams, at time in months is given by the formula . Find the number of grams present in 4 years. If necessary, round to three decimal places.
(Multiple Choice)
4.9/5  (35)
(35)
Determine whether the graph of the function is the graph of a one-to-one function.
-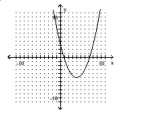
(True/False)
4.9/5  (35)
(35)
Showing 161 - 180 of 302
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)