Exam 11: Quadratic Equations and Functions
Exam 1: Review of Real Numbers490 Questions
Exam 2: Equations, Inequalities, and Problem Solving332 Questions
Exam 3: Graphing313 Questions
Exam 4: Solving Systems of Linear Equations146 Questions
Exam 5: Exponents and Polynomials304 Questions
Exam 6: Factoring Polynomials261 Questions
Exam 7: Rational Expressions327 Questions
Exam 8: More on Functions and Graphs192 Questions
Exam 9: Inequalities and Absolute Value148 Questions
Exam 10: Rational Exponents, Radicals, and Complex Numbers379 Questions
Exam 11: Quadratic Equations and Functions242 Questions
Exam 12: Exponential and Logarithmic Functions302 Questions
Exam 13: Conic Sections153 Questions
Exam 14: Sequences, Series, and the Binomial Theorem201 Questions
Select questions type
Sketch the graph of the quadratic function by finding the vertex, intercepts, and determining if the graph opens upward
or downward.
-
(Multiple Choice)
4.7/5  (37)
(37)
Solve the inequality. Graph the solution set and write the solution set in interval notation.
-

(Multiple Choice)
4.8/5  (35)
(35)
Solve the inequality. Graph the solution set and write the solution set in interval notation.
-
(Multiple Choice)
4.9/5  (49)
(49)
Solve the inequality. Graph the solution set and write the solution set in interval notation.
-

(Multiple Choice)
4.9/5  (40)
(40)
Find all numbers that satisfy the following.
-The total profit function for a company producing thousand units is given by . Find the values of for which the company makes a profit. [Hint: The company makes a profit when .]
(Multiple Choice)
4.7/5  (39)
(39)
Solve the inequality. Graph the solution set and write the solution set in interval notation.
-

(Multiple Choice)
5.0/5  (34)
(34)
Solve.
-The distance, , in feet traveled by a freely falling object is given by the function , where is time in seconds. Use this formula to find the time it would take for an object to fall to the ground from a cliff that is 1600 feet high.
(Multiple Choice)
4.8/5  (41)
(41)
Solve.
-A ball is thrown upward with an initial velocity of 35 meters per second from a cliff that is 90 meters high. The height of the ball is given by the quadratic equation where is in meters and is the time in seconds since the ball was thrown. Find the time it takes the ball to hit the ground. Round your answer to the nearest tenth of a second.
(Multiple Choice)
4.9/5  (38)
(38)
Given the accompanying graph of y = f(x), sketch the graph of the following.
-
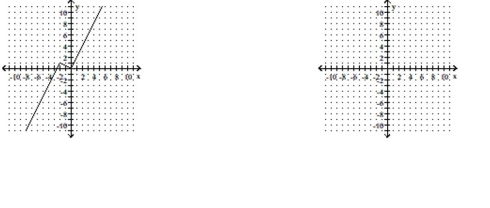
(Multiple Choice)
4.8/5  (37)
(37)
Solve the inequality. Graph the solution set and write the solution set in interval notation.
-

(Multiple Choice)
4.9/5  (44)
(44)
Sketch the graph of the quadratic function by finding the vertex, intercepts, and determining if the graph opens upward
or downward.
-
(Multiple Choice)
4.8/5  (38)
(38)
Showing 221 - 240 of 242
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)