Exam 5: Discrete Probability Distributions
Exam 1: Introduction to Statistics106 Questions
Exam 2: Summarizing and Graphing Data85 Questions
Exam 3: Statistics for Describing, Exploring, and Comparing Data187 Questions
Exam 4: Probability186 Questions
Exam 5: Discrete Probability Distributions155 Questions
Exam 6: Normal Probability Distributions227 Questions
Exam 7: Estimates and Sample Size141 Questions
Exam 8: Hypothesis Testing139 Questions
Exam 9: Inferences From Two Samples133 Questions
Exam 10: Correlation and Regression104 Questions
Exam 11: Chi-Square and Analysis of Variance65 Questions
Select questions type
Find the mean of the given probability distribution.
-The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.6561, 0.2916, 0.0486, 0.0036, and 0.0001, respectively. Round answer to the nearest hundredth.
(Multiple Choice)
4.8/5  (43)
(43)
Find the indicated probability. Round to three decimal places.
-A machine has 12 identical components which function independently. The probability that a component will fail is 0.2. The machine will stop working if more than three components fail. Find the probability that the machine will be working.
(Multiple Choice)
4.9/5  (31)
(31)
Use the given values of n and p to find the minimum usual value . Round your answer to the nearest hundredth unless otherwise noted.
-
(Multiple Choice)
4.8/5  (37)
(37)
Assume that a procedure yields a binomial distribution with a trial repeated n times. Use the binomial probability formula to find the probability of x successes given the probability p of success on a single trial. Round to three decimal places.
-
(Multiple Choice)
4.8/5  (33)
(33)
Assume that there is a 0.15 probability that a basketball playoff series will last four games, a 0.30 probability that it will last five games, a 0.25 probability that it will last six games, and a 0.30 probability that it will last seven games. Is it unusual for a team to win a series in 7 games?
(Multiple Choice)
4.8/5  (39)
(39)
Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.
- () 0 0.157 1 0.221 2 -0.060 3 0.084 4 0.166 5 0.432
(Essay)
4.8/5  (42)
(42)
Compare the probability histogram for the expected sum with the actual results. What do you conclude about the dice results displayed in the Actual Sum of Two Dice histogram?
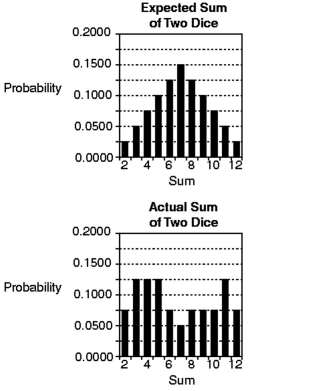
(Essay)
4.7/5  (34)
(34)
The prizes that can be won in a sweepstakes are listed below together with the chances of winning each one: $3500 (1 chance in 8800); $1400 (1 chance in 6300); $600 (1 chance in 3000); $200 (1 chance in 2900). Find the expected value of the amount won for one entry if the cost of entering is 55 cents.
(Multiple Choice)
4.9/5  (38)
(38)
Assume that a researcher randomly selects 14 newborn babies and counts the number of girls selected, x. The probabilities corresponding to the 14 possible values of x are summarized in the given table. Answer the question using
the table.
Probabilities of Girls x( girls) P(x) x (girls) P(x) x (girls) P(x) 0 0.000 5 0.122 10 0.061 1 0.001 6 0.183 11 0.022 2 0.006 7 0.209 12 0.006 3 0.022 8 0.183 13 0.001 4 0.061 9 0.122 14 0.000
-Find the probability of selecting exactly 5 girls.
(Multiple Choice)
4.8/5  (26)
(26)
Identify the given random variable as being discrete or continuous.
-The cost of a randomly selected orange
(Multiple Choice)
4.9/5  (34)
(34)
Find the mean, µ, for the binomial distribution which has the stated values of n and p. Round answer to the nearest tenth.
-
(Multiple Choice)
5.0/5  (36)
(36)
On a multiple choice test with 27 questions, each question has four possible answers, one of which is correct. For students who guess at all answers, find the variance for the number of correct answers.
(Multiple Choice)
4.8/5  (28)
(28)
Assume that a procedure yields a binomial distribution with a trial repeated n times. Use the binomial probability formula to find the probability of x successes given the probability p of success on a single trial. Round to three decimal places.
-
(Multiple Choice)
4.7/5  (33)
(33)
Determine if the outcome is unusual. Consider as unusual any result that differs from the mean by more than 2 standard deviations. That is, unusual values are either less than
-A survey for brand recognition is done and it is determined that 68% of consumers have heard of Dull Computer Company. A survey of 800 randomly selected consumers is to be conducted. For such groups of 800, would it be unusual to get 522 consumers who recognize the Dull Computer
Company name?
(Multiple Choice)
4.9/5  (40)
(40)
Use the given values of n and p to find the minimum usual value . Round
your answer to the nearest hundredth unless otherwise noted.
-
(Multiple Choice)
4.8/5  (38)
(38)
Assume that a procedure yields a binomial distribution with a trial repeated n times. Use the binomial probability formula to find the probability of x successes given the probability p of success on a single trial. Round to three decimal places.
-
(Multiple Choice)
4.9/5  (26)
(26)
On a multiple choice test with 11 questions, each question has four possible answers, one of which is correct. For students who guess at all answers, find the mean for the number of correct answers.
(Multiple Choice)
4.8/5  (38)
(38)
Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
-Choosing 8 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green) one at a time with replacement, keeping track of the colors of the marbles chosen.
(Multiple Choice)
4.8/5  (34)
(34)
Choosing 5 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green) one at a time without replacement, keeping track of the number of red marbles chosen.
(Multiple Choice)
5.0/5  (34)
(34)
In a survey of 300 college graduates, 46% reported that they entered a profession closely related to their college major. If 9 of those survey subjects are randomly selected without replacement for a follow-up survey, what is the probability that 3 of them entered a profession closely related to their
College major?
(Multiple Choice)
4.7/5  (37)
(37)
Showing 101 - 120 of 155
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)