Exam 10: Rotational Motion
Exam 1: Introduction, Measurement, Estimating71 Questions
Exam 2: Describing Motion: Kinematics in One Dimension119 Questions
Exam 3: Kinematics in Two or Three Dimensions; Vectors100 Questions
Exam 4: Dynamics: Newtons Laws of Motion86 Questions
Exam 5: Using Newtons Laws: Friction, Circular Motion, Drag Forces68 Questions
Exam 6: Gravitation and Newtons6 Synthesis64 Questions
Exam 7: Work and Energy69 Questions
Exam 8: Conservation of Energy95 Questions
Exam 9: Linear Momentum85 Questions
Exam 10: Rotational Motion99 Questions
Exam 11: Angular Momentum; General Rotation45 Questions
Exam 12: Static Equilibrium; Elasticity and Fracture61 Questions
Exam 13: Fluids112 Questions
Exam 14: Oscillations102 Questions
Exam 15: Wave Motion74 Questions
Exam 16: Sound75 Questions
Exam 17: Temperature, Thermal Expansion, and the Ideal Gas Law83 Questions
Exam 18: Kinetic Theory of Gases37 Questions
Exam 19: Heat and the First Law of Thermodynamics96 Questions
Exam 20: Second Law of Thermodynamics77 Questions
Exam 21: Electric Charge and Electric Field97 Questions
Exam 22: Gausss Law44 Questions
Exam 23: Electric Potential70 Questions
Exam 24: Capacitance, Dielectrics, Electric Energy Storage73 Questions
Exam 25: Electric Currents and Resistance71 Questions
Exam 26: Dc Circuits110 Questions
Exam 27: Magnetism102 Questions
Exam 28: Sources of Magnetic Field63 Questions
Exam 29: Electromagnetic Induction and Faradays Law116 Questions
Exam 30: Inductance, Electromagnetic Oscillations, and Ac Circuits108 Questions
Exam 31: Maxwells Equations and Electromagnetic Waves76 Questions
Exam 32: Light: Reflection and Refraction118 Questions
Exam 33: Lenses and Optical Instruments134 Questions
Exam 34: The Wave Nature of Light; Interference77 Questions
Exam 35: Diffraction and Polarization68 Questions
Exam 36: Special Theory of Relativity69 Questions
Exam 37: Early Quantum Theory and Models of the Atom95 Questions
Exam 38: Quantum Mechanics42 Questions
Exam 39: Quantum Mechanics of Atoms62 Questions
Exam 40: Molecules and Solids56 Questions
Exam 41: Nuclear Physics and Radioactivity82 Questions
Exam 42: Nuclear Energy: Efects and Uses of Radiation69 Questions
Exam 43: Elementary Particle66 Questions
Exam 44: Astrophysics and Cosmology36 Questions
Select questions type
Two children are riding on a merry-go-round. Child A is at a greater distance from the axis of rotation than child B. Which child has the larger angular speed?
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
D
A child is riding on a merry-go-round, which is accelerating. What is the relationship between the angular speed ω and the angular acceleration α of the merry-go-round when the tangential and centripetal accelerations of the child are equal?
Free
(Short Answer)
4.8/5  (32)
(32)
Correct Answer:
α = ω2
When a rigid body rotates about a fixed axis all the points in the body have the same angular displacement.
Free
(True/False)
5.0/5  (30)
(30)
Correct Answer:
True
A wheel of radius R is rolling on a horizontal surface. Its center is moving forward with speed v. A point on the wheel a distance r/3 below the center is moving forward at a speed 2v/3. The wheel is
(Multiple Choice)
4.9/5  (29)
(29)
A spool whose inner core has a radius of 1.00 cm and whose end caps have a radius of 1.50 cm has a string tightly wound around the inner core. The spool is free to roll without slipping on a horizontal surface. If the string unwinds horizontally from the bottom of the core with a constant speed of 25.0 cm/s, what is the speed of the spool?
(Multiple Choice)
4.9/5  (31)
(31)
A person pushes on a doorknob with a force of 5.00 N perpendicular to the surface of the door. The doorknob is located 0.800 m from axis of the hinges of the door. The door begins to rotate with an angular acceleration of 2.00 rad/s2. What is the moment of inertia of the door about the hinges?
(Multiple Choice)
4.9/5  (37)
(37)
A man is holding an 8.00-kg vacuum cleaner at arm's length, a distance of 0.550 m from his shoulder. What is the torque on the shoulder joint if the arm is horizontal?
(Multiple Choice)
4.8/5  (39)
(39)
Rolling without slipping depends on static friction between the rolling object and the ground.
(True/False)
4.8/5  (27)
(27)
As you are leaving a building, the door opens outward. If the hinges on the door are on your right, what is the direction of the angular velocity of the door as you open it?
(Multiple Choice)
4.7/5  (27)
(27)
Suppose a solid sphere of mass M and radius R rolls without slipping down an inclined plane starting from rest. The angular velocity of the sphere at the bottom of the incline depends on
(Multiple Choice)
4.9/5  (34)
(34)
FIGURE 10-1  -The rotating systems shown in Fig. 10-1 differ only in that the two identical movable masses are positioned a distance r from the axis of rotation (left), or a distance r/2 from the axis of rotation (right). If you release the hanging blocks simultaneously from rest,
-The rotating systems shown in Fig. 10-1 differ only in that the two identical movable masses are positioned a distance r from the axis of rotation (left), or a distance r/2 from the axis of rotation (right). If you release the hanging blocks simultaneously from rest,
(Multiple Choice)
4.9/5  (39)
(39)
When a rigid body rotates about a fixed axis all the points in the body have the same linear displacement.
(True/False)
4.7/5  (35)
(35)
Suppose a solid sphere of mass M and radius R rolls without slipping down an inclined plane starting from rest. The linear velocity of the sphere at the bottom of the incline depends on
(Multiple Choice)
4.7/5  (42)
(42)
A solid sphere of mass 1.5 kg and radius 15 cm rolls without slipping down a 35° incline that is 7.0 m long. Assume it started from rest. The moment of inertia of a sphere is given by I= (2/5)MR2.
(a) Calculate the linear speed of the sphere when it reaches the bottom of the incline.
(b) Determine the angular speed of the sphere at the bottom of the incline.
(c) Does the linear speed depend on the radius or mass of the sphere? Does the angular speed depend on the radius or mass of the sphere?
(Essay)
4.9/5  (35)
(35)
Consider a hoop of radius R and mass M rolling without slipping. Which form of kinetic energy is larger, translational or rotational?
(Multiple Choice)
4.9/5  (31)
(31)
FIGURE 10-3 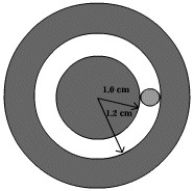 -Fig. 10-3 illustrates a simplified roller bearing. The outer hollow cylinder has a radius of 1.2 cm and is stationary. The inner cylinder has a radius of 1.0 cm and is rotating at 11 rpm. Between the two cylinders are several small cylinders with a radius of 0.10 cm, which roll without slipping on both the inner and outer cylinders. Only one of these cylinders is shown in the figure. What is the angular speed of the small cylinders?
-Fig. 10-3 illustrates a simplified roller bearing. The outer hollow cylinder has a radius of 1.2 cm and is stationary. The inner cylinder has a radius of 1.0 cm and is rotating at 11 rpm. Between the two cylinders are several small cylinders with a radius of 0.10 cm, which roll without slipping on both the inner and outer cylinders. Only one of these cylinders is shown in the figure. What is the angular speed of the small cylinders?
(Multiple Choice)
4.7/5  (30)
(30)
FIGURE 10-1  -The rotating systems shown in Fig. 10-1 differ only in that the two identical movable masses are positioned a distance r from the axis of rotation (left), or a distance r/2 from the axis of rotation (right). If you release the hanging blocks simultaneously from rest, and call tL the time taken by the block on the left and tR the time taken by the block on the right to reach the bottom, respectively, then
-The rotating systems shown in Fig. 10-1 differ only in that the two identical movable masses are positioned a distance r from the axis of rotation (left), or a distance r/2 from the axis of rotation (right). If you release the hanging blocks simultaneously from rest, and call tL the time taken by the block on the left and tR the time taken by the block on the right to reach the bottom, respectively, then
(Multiple Choice)
4.9/5  (32)
(32)
A solid disk is released from rest and rolls without slipping down an inclined plane that makes an angle of 25.0° with the horizontal. What is the speed of the disk after it has rolled 3.00 m, measured along the plane?
(Multiple Choice)
4.8/5  (36)
(36)
A string is wrapped around a pulley with a radius of 2.0 cm. The pulley is initially at rest. A constant force of 50 N is applied to the string, causing the pulley to rotate and the string to unwind. If the string unwinds 1.2 m in 4.9 s, what is the moment of inertia of the pulley?
(Multiple Choice)
4.8/5  (36)
(36)
The moment of inertia of a uniform rod (about its center) is given by I = M 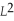 /12. What is the kinetic energy of a 120-cm rod with a mass of 450 g rotating about its center at 3.60 rad/s?
/12. What is the kinetic energy of a 120-cm rod with a mass of 450 g rotating about its center at 3.60 rad/s?
(Multiple Choice)
4.9/5  (39)
(39)
Showing 1 - 20 of 99
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)