Exam 4: Polynomial and Rational Functions
Exam 1: Graphs, Functions, and Models189 Questions
Exam 2: More on Functions157 Questions
Exam 3: Quadratic Functions and Equations; Inequalities209 Questions
Exam 4: Polynomial and Rational Functions94 Questions
Exam 5: Exponential and Logarithmic Functions106 Questions
Exam 6: Systems of Equations and Matrices70 Questions
Exam 7: Conic Sections59 Questions
Exam 8: Sequences, Series, and Combinatorics92 Questions
Select questions type
Solve.
-There are people in a room. The number of possible handshakes by all the people in the room is given by the function . For what number n of people is ?
(Multiple Choice)
4.7/5  (43)
(43)
For the function find the maximum number of real zeros that the function can have, the maximum number of x-intercepts
that the function can have, and the maximum number of turning points that the graph of the function can have.
-
(Multiple Choice)
4.8/5  (35)
(35)
List the critical values of the related function. Then solve the inequality.
-
(Multiple Choice)
4.9/5  (33)
(33)
Given that the polynomial function has the given zero, find the other zeros.
-
(Multiple Choice)
4.9/5  (29)
(29)
List the critical values of the related function. Then solve the inequality.
-
(Multiple Choice)
4.8/5  (42)
(42)
Find the zeros of the polynomial function and state the multiplicity of each.
-
(Multiple Choice)
4.7/5  (37)
(37)
Solve the problem.
-A stone thrown downward with an initial velocity of will travel a distance of meters, where and is in seconds. If a stone is thrown downward at from a height of , how long will it take the stone to hit the ground? Round your answer to the nearest second.
(Multiple Choice)
4.9/5  (31)
(31)
Solve the given inequality (a related function is graphed).
-
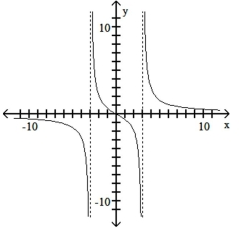
(Multiple Choice)
4.7/5  (33)
(33)
Use Descartes' Rule of Signs to determine the possible number of positive real zeros and the possible number of negative
real zeros for the function.
-
(Multiple Choice)
4.8/5  (41)
(41)
Use the leading-term test to match the function with the correct graph.
-
(Multiple Choice)
4.8/5  (35)
(35)
List the critical values of the related function. Then solve the inequality.
-
(Multiple Choice)
4.9/5  (40)
(40)
Find the correct end behavior diagram for the given polynomial function.
-

(Short Answer)
5.0/5  (41)
(41)
Classify the polynomial as constant, linear, quadratic, cubic, or quartic, and determine the leading term, the leading
coefficient, and the degree of the polynomial.
-
(Multiple Choice)
4.8/5  (40)
(40)
Solve.
-An open-top rectangular box has a square base and it will hold 256 cubic centimeters (cc). Each side of the base has length . The box's surface area is given by
Estimate the minimum surface area and the value of that will yield it.
(Multiple Choice)
4.7/5  (40)
(40)
Showing 21 - 40 of 94
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)