Exam 2: More on Functions

Graph the function. -

For the piecewise function, find the specified function value. - $f ( x ) = \left\{ \begin{array} { l l } 6 x , & \text { for } x \leq - 1 \\x - 5 , & \text { for } x > - 1\end{array} \right.$ f(-7)

Solve the problem. -Ken is 6 feet tall and is walking away from a streetlight. The streetlight has its light bulb 14 feet above the ground, and Ken is walking at the rate of 1.9 feet per second. Find a function, d(t), which gives the distance Ken is from the streetlight in terms of time. Find a function, S(d), which gives the length of Ken's shadow in terms of d. Then find $( S \circ \mathrm { d } ) ( \mathrm { t } ) = 3.21 \mathrm { t }$

Graph the equation. -

Solve the problem. -The current I in an electrical conductor varies inversely as the resistance R of the conductor. The current is 7 amperes when the resistance is 765 ohms. What is the current when the resistance is 777 Ohms?

Solve. -The weight of a liquid varies directly as its volume V. If the weight of the liquid in a cubical container 5 cm on a side is 375 g, find the weight of the liquid in a cubical container 3 cm on a Side.

Solve the problem. -The amount of tread left on a tire varies inversely as the number of miles the tire has traveled. A tire that has traveled 93,000 miles has 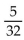inches of tread left. How much tread will be left on a tire that has traveled 23,000 miles?

Answer the question. -How can the graph of $f ( x ) = \frac { 7 } { x } + 4$ be obtained from the graph of $y = \frac { 1 } { x } ?$ A) Shrink it vertically a factor of $\frac { 1 } { 7 } .$ Shift it 4 units up. B) Shift it horizontally 7 units to the left. Shift it 4 units down. C) Shift it horizontally 7 units to the right. Shift it 4 units up. D) Stretch it vertically by a factor of 7 . Shift it 4 units up.

Write an equation for a function that has a graph with the given characteristics. -The shape of $y = \sqrt { x }$ is shifted 6 units to the left. Then the graph is shifted 8 units upward.

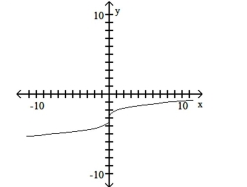
Determine the intervals on which the function is increasing, decreasing, and constant. -

Answer the question. -How can the graph of $f ( x ) = \frac { 1 } { - x } - 1$ be obtained from the graph of $y = \frac { 1 } { x } ?$

Find an equation of variation for the given situation. - y varies directly as the square of x , and y=8.75 when x=5 .

Answer the question. -How can the graph of $f ( x ) = - \sqrt [ 3 ] { x + 8 }$ be obtained from the graph of $y = \sqrt [ 3 ] { x } ?$ A) Shift it vertically 8 units upward. Reflect it across the x -axis. B) Shift it horizontally 8 units to the left. Reflect it across the y-axis. C) Shift it horizontally 8 units to the left. Reflect it across the x -axis.

Find an equation of variation for the given situation. - y varies jointly as x and the square of z , and y=209.9072 when x=0.8 and z=4.6

Find the requested function value. - $f ( x ) = 8 x - 2 , g ( x ) = - 3 x ^ { 2 } - 5 x - 4$ Find $\left( \begin{array} { l l } g & \text { o }f\end{array} \right) ( - 9 )$ A) -16,062 B) -1618 C) 542 D) 588

Determine algebraically whether the graph is symmetric with respect to the x-axis, the y-axis, and the origin. - $x ^ { 2 } + 5 y ^ { 4 } = 2$

Find an equation of variation for the given situation. - y varies jointly as x and z , and y=18 when x=3 and z=3

Find an equation of variation for the given situation. -y varies inversely as x and y =5.25 when x=0.36

Graph the function. -

Solve. -A rectangular box with volume 468 cubic feet is built with a square base and top. The cost is $1.50 per square foot for the top and the bottom and $2.00 per square foot for the sides. Let x represent the length of a side of the base in feet. Express the cost of the box as a function of x and then graph this function. From the graph find the value of x, to the nearest hundredth of a foot, which will minimize the cost of the box.