Exam 14: Inference for Regression
Exam 1: Data and Decisions41 Questions
Exam 2: Displaying and Describing Categorical Data45 Questions
Exam 3: Displaying and Describing Quantitative Data32 Questions
Exam 4: Correlation and Linear Regression84 Questions
Exam 5: Randomness and Probability34 Questions
Exam 6: Random Variables and Probability Models28 Questions
Exam 7: The Normal and Other Continuous Distributions31 Questions
Exam 8: Surveys and Sampling30 Questions
Exam 9: Sampling Distributions and Confidence Intervals for Proportions66 Questions
Exam 10: Testing Hypotheses About Proportions27 Questions
Exam 11: Confidence Intervals and Hypothesis Tests for Means28 Questions
Exam 12: Comparing Two Means35 Questions
Exam 13: Inference for Counts: Chi-Square Tests68 Questions
Exam 14: Inference for Regression38 Questions
Exam 15: Multiple Regression36 Questions
Exam 16: Introduction to Data Mining68 Questions
Select questions type
Use the following for questions
A sales manager was interested in determining if there is a relationship between college GPA and sales performance among salespeople hired within the last year. A sample of recently hired salespeople was selected and college GPA and the number of units sold last month recorded. Below are the scatterplot, regression results, and residual plots for these data. The regression equation is
Units Sold GPA
Predictor Coef SE Coef T P Constant -0.484 3.256 -0.15 0.884 GPA 7.423 1.044 7.11 0.000
Analysis of Variance
Source DF SS MS F P Regression 1 125.30 125.30 50.56 0.000 Residual Error 14 34.70 2.48 Total 15 160.00 Answer: 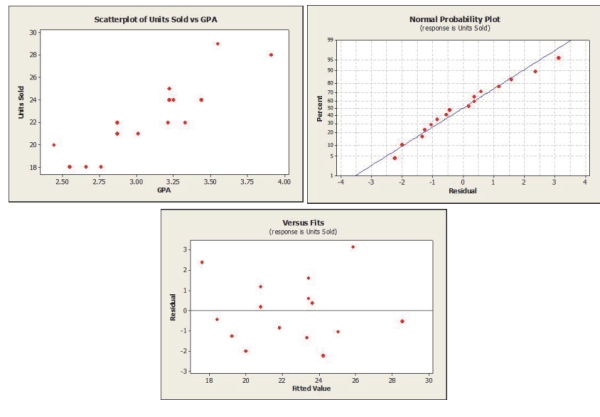 -What is the independent variable in this regression? Write the null and alternative
hypothesis to test the slope of this variable.
-What is the independent variable in this regression? Write the null and alternative
hypothesis to test the slope of this variable.
Free
(Essay)
4.8/5  (33)
(33)
Correct Answer:
The independent variable is GPA
Ho: There is no association between GPA and sales performance.
: There is an association between GPA and sales performance.
A regression equation was fit to the data showing the number of hours of training time received by production line workers and the time it took (in minutes) for them to
Trouble shoot their last process problem and the following histogram of residuals
Obtained. Based on this histogram of the residuals, we can say that the: 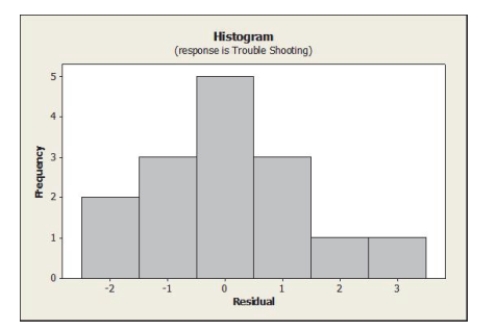
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
A
Based on the scatterplot of data of the number of hours of training time received by production line workers and the time it took (in minutes) for them to trouble shoot
Their last process problem shown, we can say that 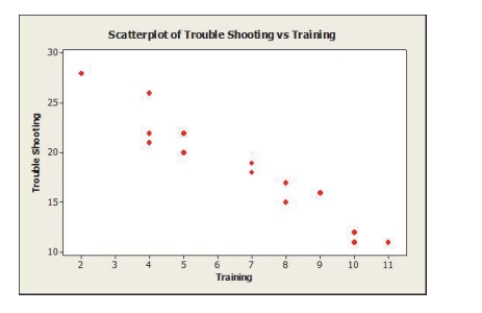
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
B
Use the following for questions
An operations manager was interested in determining if there is a relationship between the amount of training received by production line workers and the time it takes for them to troubleshoot a process problem. A sample of recently trained line workers was selected. The number of hours of training time received and the time it took (in minutes) for them to troubleshoot their last process problem were captured. Below are the scatterplot, regression results, and residual plots for these data. The regression equation is
Trouble Shooting Training
Predictor Coef SE Coef T P Constant 30.729 1.023 30.03 0.000 Training -1.8360 0.1376 -13.35 0.000
Analysis of Variance
Source DF SS MS F P Regression 1 367.20 367.20 178.10 0.000 Residual Error 13 26.80 2.06 Total 14 394.00
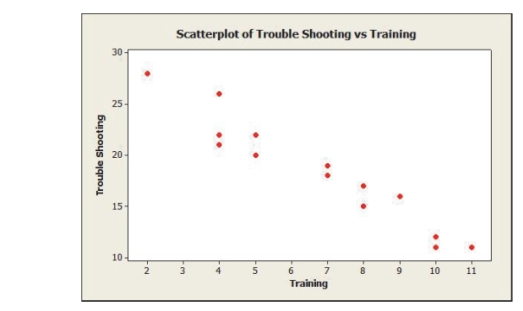 -The 95% confidence interval for troubleshooting time with 8 hours of training is
(15.180, 16.903). Interpret this interval with respect to the estimated troubleshooting
time.
-The 95% confidence interval for troubleshooting time with 8 hours of training is
(15.180, 16.903). Interpret this interval with respect to the estimated troubleshooting
time.
(Essay)
4.7/5  (33)
(33)
A researcher is interested in developing a model that can be used to distribute assistance to low income families for food costs. She used data from a national social Survey to predict weekly amount spent on food using household income (in $1000).
The resulting regression equation is How Much money would be needed to feed a family for a week whose household income Is $12,000?
(Multiple Choice)
4.9/5  (39)
(39)
In a significant regression model determining if there is a relationship between college GPA and sales performance (number of units sold in the previous month), the 95% confidence interval for the number of units sold when GPA = 3.00 was
Determined to be 20.914 to 22.657. The correct interpretation is
(Multiple Choice)
4.8/5  (40)
(40)
A researcher gathers data on the length of essays (number of lines) and the SAT scores received for a sample of students enrolled at his university. Based on his
Regression results, the 95% confidence interval for the slope of the regression
Equation is -0.88 to 1.34. At α = 0.05, we can say
(Multiple Choice)
4.9/5  (30)
(30)
Use the following for questions
A sales manager was interested in determining if there is a relationship between college GPA and sales performance among salespeople hired within the last year. A sample of recently hired salespeople was selected and college GPA and the number of units sold last month recorded. Below are the scatterplot, regression results, and residual plots for these data. The regression equation is
Units Sold GPA
Predictor Coef SE Coef T P Constant -0.484 3.256 -0.15 0.884 GPA 7.423 1.044 7.11 0.000
Analysis of Variance
Source DF SS MS F P Regression 1 125.30 125.30 50.56 0.000 Residual Error 14 34.70 2.48 Total 15 160.00 Answer:  -The confidence interval and prediction interval for the number of units sold per
month when GPA = 3.00 are shown below. Write a sentence to interpret each
interval in this context.
-The confidence interval and prediction interval for the number of units sold per
month when GPA = 3.00 are shown below. Write a sentence to interpret each
interval in this context.
(Essay)
4.9/5  (35)
(35)
Use the following information for questions
Nutritional information was collected for 77 breakfast cereals including the amount of fiber (in grams), potassium (in mg), and the number of calories per serving. The data resulted in the following scatterplots.
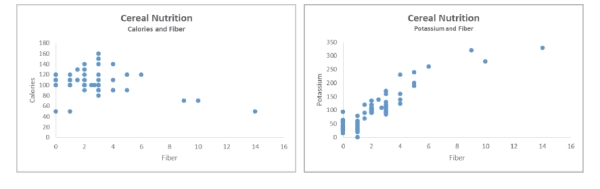 -From which of these plots would you expect a more consistent regression slope estimate? Why?
-From which of these plots would you expect a more consistent regression slope estimate? Why?
(Essay)
4.8/5  (39)
(39)
Use the following for questions
A sales manager was interested in determining if there is a relationship between college GPA and sales performance among salespeople hired within the last year. A sample of recently hired salespeople was selected and college GPA and the number of units sold last month recorded. Below are the scatterplot, regression results, and residual plots for these data. The regression equation is
Units Sold GPA
Predictor Coef SE Coef T P Constant -0.484 3.256 -0.15 0.884 GPA 7.423 1.044 7.11 0.000
Analysis of Variance
Source DF SS MS F P Regression 1 125.30 125.30 50.56 0.000 Residual Error 14 34.70 2.48 Total 15 160.00 Answer:  -Circle the standard error of the slope and its components in the output shown. If the
information is not in the output, list components.
-Circle the standard error of the slope and its components in the output shown. If the
information is not in the output, list components.
(Essay)
4.7/5  (28)
(28)
Which of the following does NOT affect the standard error of the regression slope?
(Multiple Choice)
4.8/5  (32)
(32)
Use the following information for questions
Nutritional information was collected for 77 breakfast cereals including the amount of fiber (in grams), potassium (in mg), and the number of calories per serving. The data resulted in the following scatterplots.
 -Compare the two plots with respect to the aspects that would affect the standard error
of the regression slope?
-Compare the two plots with respect to the aspects that would affect the standard error
of the regression slope?
(Essay)
4.7/5  (28)
(28)
Use the following for questions
An operations manager was interested in determining if there is a relationship between the amount of training received by production line workers and the time it takes for them to troubleshoot a process problem. A sample of recently trained line workers was selected. The number of hours of training time received and the time it took (in minutes) for them to troubleshoot their last process problem were captured. Below are the scatterplot, regression results, and residual plots for these data. The regression equation is
Trouble Shooting Training
Predictor Coef SE Coef T P Constant 30.729 1.023 30.03 0.000 Training -1.8360 0.1376 -13.35 0.000
Analysis of Variance
Source DF SS MS F P Regression 1 367.20 367.20 178.10 0.000 Residual Error 13 26.80 2.06 Total 14 394.00
 -Write a sentence to interpret the coefficient of training in the regression equation.
-Write a sentence to interpret the coefficient of training in the regression equation.
(Essay)
4.8/5  (34)
(34)
Cars from an online service were examined to see how fuel efficiency (highway mpg) relates to cost (in dollars). According to the regression equation, a used car that costs
$13,000 is predicted to get about 30.24 miles per gallon. According to the data, the
Car got 35 miles per gallon. What is the value of the residual for this car?
(Multiple Choice)
4.9/5  (40)
(40)
As the carbon content in steel increases, its ductility tends to decrease. A researcher at a steel company measures carbon content and ductility for a sample of 15 types of
Steel. Based on these data he obtained the following regression results, which of the
Following statements is NOT true? The regression equation is
Ductility Carbon Content
Predictor Coef SE Coef T P Constant 7.671 1.507 5.09 0.000 Carbon Content -3.296 1.097 -3.01 0.010
(Multiple Choice)
5.0/5  (32)
(32)
An estimated regression equation that was fit to estimate ductility in steel using its carbon content was found to be significant at α = 0.05. The 95% prediction interval
For the ductility of steel with 0.5% carbon content was determined to be 0.45 to 11.59.
The correct interpretation is
(Multiple Choice)
4.9/5  (39)
(39)
Use the following for questions
An operations manager was interested in determining if there is a relationship between the amount of training received by production line workers and the time it takes for them to troubleshoot a process problem. A sample of recently trained line workers was selected. The number of hours of training time received and the time it took (in minutes) for them to troubleshoot their last process problem were captured. Below are the scatterplot, regression results, and residual plots for these data. The regression equation is
Trouble Shooting Training
Predictor Coef SE Coef T P Constant 30.729 1.023 30.03 0.000 Training -1.8360 0.1376 -13.35 0.000
Analysis of Variance
Source DF SS MS F P Regression 1 367.20 367.20 178.10 0.000 Residual Error 13 26.80 2.06 Total 14 394.00
 -Is there a significant relationship between time it takes to troubleshoot the process(minutes) and training received (use α = .05)? Give the appropriate test statistic,associated P-value, and conclusion.
-Is there a significant relationship between time it takes to troubleshoot the process(minutes) and training received (use α = .05)? Give the appropriate test statistic,associated P-value, and conclusion.
(Essay)
4.8/5  (35)
(35)
A sample of 15 recently trained line workers was selected to determine if there is a relationship between the number of hours of training time received by production line
Workers and the time it took (in minutes) for them to trouble shoot their last process
Problem were captured. Use the regression output for the independent variable
Shown below to find the 95% confidence interval for the slope of the regression Equation.
(Multiple Choice)
4.9/5  (35)
(35)
As the carbon content in steel increases, its ductility tends to decrease. A researcher at a steel company measures carbon content and ductility for a sample of 15 types ofsteel. Use the following regression results to find the 95% confidence interval for the
Slope of the regression equation. Predictor Coef SE Coef T P Constant 7.671 1.507 5.09 0.000 Carbon Content -3.296 1.097 -3.01 0.010
(Multiple Choice)
5.0/5  (43)
(43)
Use the following for questions
An operations manager was interested in determining if there is a relationship between the amount of training received by production line workers and the time it takes for them to troubleshoot a process problem. A sample of recently trained line workers was selected. The number of hours of training time received and the time it took (in minutes) for them to troubleshoot their last process problem were captured. Below are the scatterplot, regression results, and residual plots for these data. The regression equation is
Trouble Shooting Training
Predictor Coef SE Coef T P Constant 30.729 1.023 30.03 0.000 Training -1.8360 0.1376 -13.35 0.000
Analysis of Variance
Source DF SS MS F P Regression 1 367.20 367.20 178.10 0.000 Residual Error 13 26.80 2.06 Total 14 394.00
 -Based on the scatterplot, what is the relationship between training and troubleshooting? Is a regression appropriate for this data? Why or why not?
-Based on the scatterplot, what is the relationship between training and troubleshooting? Is a regression appropriate for this data? Why or why not?
(Essay)
4.9/5  (22)
(22)
Showing 1 - 20 of 38
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)