Exam 10: Probability and Calculus
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
Find the value of the probability of the standard normal variable Z. Round your answer to four decimal places. 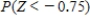
(Multiple Choice)
4.9/5  (34)
(34)
Find the median of the random variable x with the probability density function defined on the indicated interval I. The median of x is defined to be the number m such that 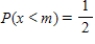 . Observe that half of the x-values lie below m and the other half lie above m. Round the answer to two decimal places, if necessary.
. Observe that half of the x-values lie below m and the other half lie above m. Round the answer to two decimal places, if necessary.
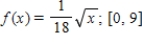
(Short Answer)
4.8/5  (33)
(33)
Let Z be the standard normal variable. Round your answers to the nearest hundredth, if necessary.
Find the value of z if z satisfies 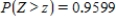 .
.
 __________
Find the value of z if z satisfies
__________
Find the value of z if z satisfies 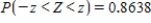 .
.
 __________
__________
(Short Answer)
4.8/5  (46)
(46)
Find the value of the constant k so that the function is a probability density function in the indicated interval. 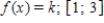
(Multiple Choice)
4.7/5  (38)
(38)
Suppose X is a normal random variable with 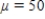 and
and 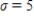 . Round your answers to four decimal places, if necessary.
Find
. Round your answers to four decimal places, if necessary.
Find 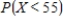 .
.
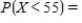 __________
Find
__________
Find 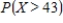 .
.
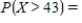 __________
Find
__________
Find 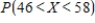 .
.
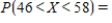 __________
__________
(Short Answer)
4.9/5  (41)
(41)
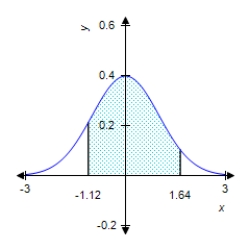
Find the value of the probability of the standard normal variable Z corresponding to the shaded area under the standard normal curve. Round your answer to four decimal places. 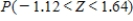
(Multiple Choice)
4.8/5  (33)
(33)
Find the value of the constant k so that the function is a probability density function in the indicated interval.
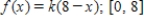
(Short Answer)
4.8/5  (35)
(35)
Find the value of the constant k so that the function is a joint probability density function on D.
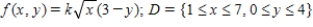
(Short Answer)
4.8/5  (33)
(33)
Find the mean of the random variable x associated with the probability density function over the indicated interval. 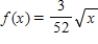 ;
; 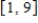
(Multiple Choice)
4.8/5  (34)
(34)
Find the median of the random variable x with the probability density function defined on the indicated interval I. The median of x is defined to be the number m such that 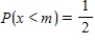 . Observe that half of the x-values lie below m and the other half lie above m.
. Observe that half of the x-values lie below m and the other half lie above m.
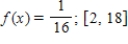
 __________
__________
(Short Answer)
4.9/5  (34)
(34)
Find the median of the random variable x with the probability density function defined on the indicated interval I. The median of x is defined to be the number m such that 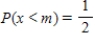 . Observe that half of the x-values lie below m and the other half lie above m. Round the answer to two decimal places, if necessary.
. Observe that half of the x-values lie below m and the other half lie above m. Round the answer to two decimal places, if necessary.
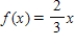 ;
; 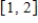
(Short Answer)
4.9/5  (39)
(39)
Find the mean of the random variable x associated with the probability density function over the indicated interval. 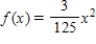 ;
; 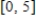
(Multiple Choice)
4.8/5  (42)
(42)
According to data released by a city's Chamber of Commerce, the weekly wages (in dollars) of female factory workers are normally distributed with a mean of 470 and a standard deviation of 50. Find the probability that a female factory worker selected at random from the city has a weekly wage of $450 to $550.
Round your answer to four decimal places.
(Short Answer)
4.9/5  (30)
(30)
Find the value of the constant k so that the function is a probability density function in the indicated interval.
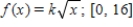
(Short Answer)
4.8/5  (26)
(26)
Find the value of the probability of the standard normal variable Z corresponding to the shaded area under the standard normal curve. Round your answer to four decimal places.
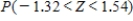
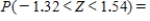 __________
__________
(Short Answer)
5.0/5  (29)
(29)
National Welding Company uses industrial robots in some of its assembly-line operations. Management has determined that the lengths of time in hours between breakdowns are exponentially distributed with probability density function
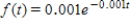
What is the probability that a robot selected at random will break down between 500 and 800 hr of use? Round the answer to the nearest hundredth.
__________
What is the probability that a robot will break down after 1,100 hr of use? Round the answer to the nearest hundredth.
__________
What is the probability that a robot selected at random will break down between 500 and 800 hr of use? Round the answer to the nearest hundredth.
__________
What is the probability that a robot will break down after 1,100 hr of use? Round the answer to the nearest hundredth.
__________
(Short Answer)
4.7/5  (34)
(34)
The tread lives of Super Titan radial tires under normal driving conditions are normally distributed with a mean of 42,000 mi and a standard deviation of 5,000 mi. What is the probability that a tire selected at random will have a tread life of more than 35,000 mi? Round your answer to four decimal places, if necessary.
__________
If four new tires are installed on a car and they experience even wear, determine the probability that all four tires still have useful tread lives after 35,000 mi of driving. Round your answer to four decimal places, if necessary.
__________
(Short Answer)
4.8/5  (31)
(31)
Find the median of the random variable x with the probability density function defined on the indicated interval I. The median of x is defined to be the number m such that 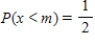 . Observe that half of the x-values lie below m and the other half lie above m.
. Observe that half of the x-values lie below m and the other half lie above m. 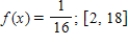
(Multiple Choice)
4.9/5  (38)
(38)
The amount of snowfall in feet in a remote region of Alaska in the month of January is a continuous random variable with probability density function 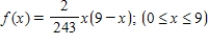
Find the amount of snowfall one can expect in any given month of January in Alaska.
Find the amount of snowfall one can expect in any given month of January in Alaska.
(Multiple Choice)
4.8/5  (41)
(41)
National Welding Company uses industrial robots in some of its assembly-line operations. Management has determined that the lengths of time in hours between breakdowns are exponentially distributed with probability density function 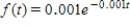 .
What is the probability that a robot selected at random will break down between 400 and 500 hr of use? Round your answer to the nearest hundredth.
.
What is the probability that a robot selected at random will break down between 400 and 500 hr of use? Round your answer to the nearest hundredth.
(Multiple Choice)
4.8/5  (31)
(31)
Showing 41 - 60 of 68
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)