Exam 15: Multiple Regression Model Building
Exam 1: Introduction145 Questions
Exam 2: Organizing and Visualizing Data210 Questions
Exam 3: Numerical Descriptive Measures153 Questions
Exam 4: Basic Probability171 Questions
Exam 5: Discrete Probability Distributions218 Questions
Exam 6: The Normal Distribution and Other Continuous Distributions191 Questions
Exam 7: Sampling and Sampling Distributions197 Questions
Exam 8: Confidence Interval Estimation196 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests165 Questions
Exam 10: Two-Sample Tests210 Questions
Exam 11: Analysis of Variance213 Questions
Exam 12: Chi-Square Tests and Nonparametric Tests201 Questions
Exam 13: Simple Linear Regression213 Questions
Exam 14: Introduction to Multiple Regression355 Questions
Exam 15: Multiple Regression Model Building96 Questions
Exam 16: Time-Series Forecasting168 Questions
Exam 17: Statistical Applications in Quality Management133 Questions
Exam 18: A Roadmap for Analyzing Data54 Questions
Exam 19: Questions that Involve Online Topics321 Questions
Select questions type
TABLE 15-5
What are the factors that determine the acceleration time (in sec.)from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu.ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The coefficient of multiple determination (R 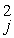 )for the regression model using each of the 5 variables Xⱼ as the dependent variable and all other X variables as independent variables are,respectively,0.7461,0.5676,0.6764,0.8582,0.6632.
-Referring to Table 15-5,what is the value of the variance inflationary factor of Cargo Vol?
)for the regression model using each of the 5 variables Xⱼ as the dependent variable and all other X variables as independent variables are,respectively,0.7461,0.5676,0.6764,0.8582,0.6632.
-Referring to Table 15-5,what is the value of the variance inflationary factor of Cargo Vol?
(Short Answer)
4.8/5  (37)
(37)
One of the consequences of collinearity in multiple regression is inflated standard errors in some or all of the estimated slope coefficients.
(True/False)
4.8/5  (33)
(33)
The stepwise regression approach takes into consideration all possible models.
(True/False)
4.8/5  (43)
(43)
One of the consequences of collinearity in multiple regression is biased estimates on the slope coefficients.
(True/False)
5.0/5  (33)
(33)
Collinearity will result in excessively low standard errors of the parameter estimates reported in the regression output.
(True/False)
4.9/5  (39)
(39)
TABLE 15-3
A chemist employed by a pharmaceutical firm has developed a muscle relaxant.She took a sample of 14 people suffering from extreme muscle constriction.She gave each a vial containing a dose (X)of the drug and recorded the time to relief (Y)measured in seconds for each.She fit a "centered" curvilinear model to this data.The results obtained by Microsoft Excel follow,where the dose (X)given has been "centered."
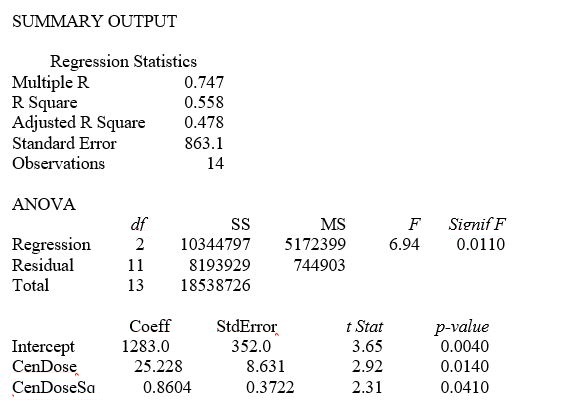 -Referring to Table 15-3,suppose the chemist decides to use a t test to determine if there is a significant difference between a linear model and a curvilinear model that includes a linear term.The p-value of the test statistic for the contribution of the curvilinear term is ________.
-Referring to Table 15-3,suppose the chemist decides to use a t test to determine if there is a significant difference between a linear model and a curvilinear model that includes a linear term.The p-value of the test statistic for the contribution of the curvilinear term is ________.
(Short Answer)
4.9/5  (35)
(35)
TABLE 15-1
A certain type of rare gem serves as a status symbol for many of its owners.In theory,for low prices,the demand increases and it decreases as the price of the gem increases.However,experts hypothesize that when the gem is valued at very high prices,the demand increases with price due to the status owners believe they gain in obtaining the gem.Thus,the model proposed to best explain the demand for the gem by its price is the quadratic model:
Y = β₀ + β₁X + β₁X² + ε
where Y = demand (in thousands)and X = retail price per carat.
This model was fit to data collected for a sample of 12 rare gems of this type.A portion of the computer analysis obtained from Microsoft Excel is shown below:
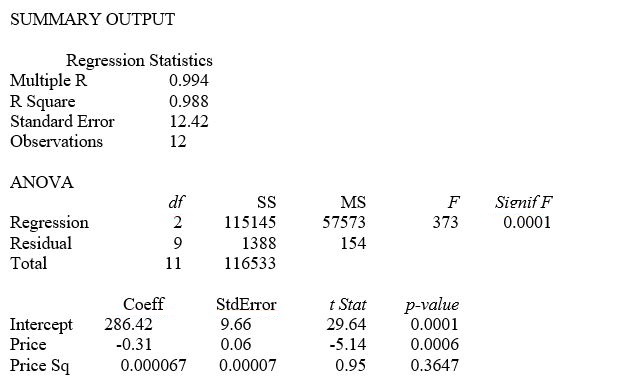 -Referring to Table 15-1,what is the correct interpretation of the coefficient of multiple determination?
-Referring to Table 15-1,what is the correct interpretation of the coefficient of multiple determination?
(Multiple Choice)
4.7/5  (39)
(39)
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y)and the independent variables are the age of the worker (X₁),the number of years of education received (X₂),the number of years at the previous job (X₃),a dummy variable for marital status (X₄: 1 = married,0 = otherwise),a dummy variable for head of household (X₅: 1 = yes,0 = no)and a dummy variable for management position (X₆: 1 = yes,0 = no).
The coefficient of multiple determination (R2J )for the regression model using each of the 6 variables Xⱼ as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:
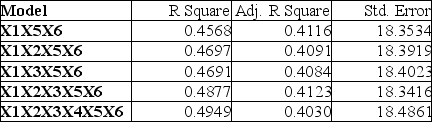 -Referring to Table 15-6,what is the value of the Mallow's Cp statistic for the model that includes X₁,X₂,X₃,X₅ and X₆?
-Referring to Table 15-6,what is the value of the Mallow's Cp statistic for the model that includes X₁,X₂,X₃,X₅ and X₆?
(Short Answer)
4.8/5  (48)
(48)
TABLE 15-6
Given below are results from the regression analysis on 40 observations where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Y)and the independent variables are the age of the worker (X₁),the number of years of education received (X₂),the number of years at the previous job (X₃),a dummy variable for marital status (X₄: 1 = married,0 = otherwise),a dummy variable for head of household (X₅: 1 = yes,0 = no)and a dummy variable for management position (X₆: 1 = yes,0 = no).
The coefficient of multiple determination (R2J )for the regression model using each of the 6 variables Xⱼ as the dependent variable and all other X variables as independent variables are,respectively,0.2628,0.1240,0.2404,0.3510,0.3342 and 0.0993.
The partial results from best-subset regression are given below:
 -Referring to Table 15-6,what is the value of the variance inflationary factor of Head?
-Referring to Table 15-6,what is the value of the variance inflationary factor of Head?
(Short Answer)
4.8/5  (31)
(31)
A microeconomist wants to determine how corporate sales are influenced by capital and wage spending by companies.She proceeds to randomly select 26 large corporations and record information in millions of dollars.A statistical analyst discovers that capital spending by corporations has a significant inverse relationship with wage spending.What should the microeconomist who developed this multiple regression model be particularly concerned with?
(Multiple Choice)
4.8/5  (35)
(35)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state.
Let Y = % Passing as the dependent variable,X₁ = % Attendance,X₂ = Salaries and X₃ = Spending.
The coefficient of multiple determination (R 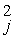 )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
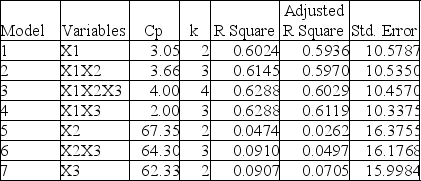
The output from the best-subset regressions is given below:
)of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below:
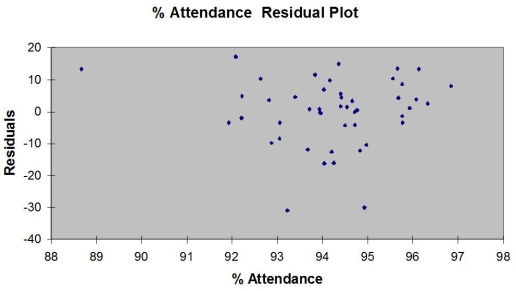
 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
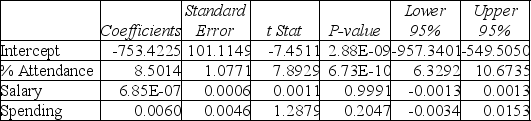
 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):
 Model (II):
Model (II):
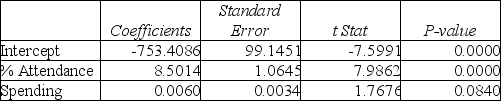 Model (III):
Model (III):
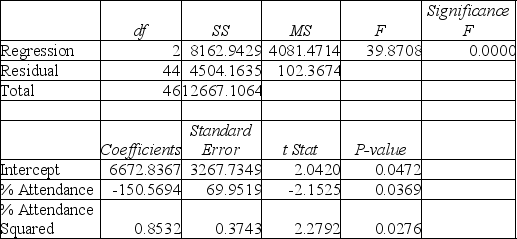 -Referring to Table 15-4,the "best" model using a 5% level of significance among those chosen by the Cp statistic is
-Referring to Table 15-4,the "best" model using a 5% level of significance among those chosen by the Cp statistic is
(Multiple Choice)
4.8/5  (24)
(24)
TABLE 15-3
A chemist employed by a pharmaceutical firm has developed a muscle relaxant.She took a sample of 14 people suffering from extreme muscle constriction.She gave each a vial containing a dose (X)of the drug and recorded the time to relief (Y)measured in seconds for each.She fit a "centered" curvilinear model to this data.The results obtained by Microsoft Excel follow,where the dose (X)given has been "centered."
 -Referring to Table 15-3,suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose.The p-value of the test is ________.
-Referring to Table 15-3,suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose.The p-value of the test is ________.
(Short Answer)
4.8/5  (28)
(28)
TABLE 15-2
In Hawaii,condemnation proceedings are under way to enable private citizens to own the property that their homes are built on.Until recently,only estates were permitted to own land,and homeowners leased the land from the estate.In order to comply with the new law,a large Hawaiian estate wants to use regression analysis to estimate the fair market value of the land.The following model was fit to data collected for n = 20 properties,10 of which are located near a cove.
 -Referring to Table 15-2,given a quadratic relationship between sale price (Y)and property size (X₁),what test should be used to test whether the curves differ from cove and non-cove properties?
-Referring to Table 15-2,given a quadratic relationship between sale price (Y)and property size (X₁),what test should be used to test whether the curves differ from cove and non-cove properties?
(Multiple Choice)
4.8/5  (36)
(36)
A real estate builder wishes to determine how house size (House)is influenced by family income (Income),family size (Size),and education of the head of household (School).House size is measured in hundreds of square feet,income is measured in thousands of dollars,and education is in years.The builder randomly selected 50 families and constructed the multiple regression model.The business literature involving human capital shows that education influences an individual's annual income.Combined,these may influence family size.With this in mind,what should the real estate builder be particularly concerned with when analyzing the multiple regression model?
(Multiple Choice)
4.8/5  (36)
(36)
TABLE 15-3
A chemist employed by a pharmaceutical firm has developed a muscle relaxant.She took a sample of 14 people suffering from extreme muscle constriction.She gave each a vial containing a dose (X)of the drug and recorded the time to relief (Y)measured in seconds for each.She fit a "centered" curvilinear model to this data.The results obtained by Microsoft Excel follow,where the dose (X)given has been "centered."
 -Referring to Table 15-3,suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose.The value of the test statistic is ________.
-Referring to Table 15-3,suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose.The value of the test statistic is ________.
(Short Answer)
4.7/5  (31)
(31)
TABLE 15-2
In Hawaii,condemnation proceedings are under way to enable private citizens to own the property that their homes are built on.Until recently,only estates were permitted to own land,and homeowners leased the land from the estate.In order to comply with the new law,a large Hawaiian estate wants to use regression analysis to estimate the fair market value of the land.The following model was fit to data collected for n = 20 properties,10 of which are located near a cove.
 -Referring to Table 15-2,given a quadratic relationship between sale price (Y)and property size (X₁),what null hypothesis would you test to determine whether the curves differ from cove and non-cove properties?
-Referring to Table 15-2,given a quadratic relationship between sale price (Y)and property size (X₁),what null hypothesis would you test to determine whether the curves differ from cove and non-cove properties?
(Multiple Choice)
4.9/5  (31)
(31)
The goals of model building are to find a good model with the fewest independent variables that is easier to interpret and has lower probability of collinearity.
(True/False)
4.9/5  (33)
(33)
In multiple regression,the ________ procedure permits variables to enter and leave the model at different stages of its development.
(Short Answer)
4.8/5  (40)
(40)
Collinearity is present when there is a high degree of correlation between independent variables.
(True/False)
4.8/5  (32)
(32)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing),daily mean of the percentage of students attending class (% Attendance),mean teacher salary in dollars (Salaries),and instructional spending per pupil in dollars (Spending)of 47 schools in the state.
Let Y = % Passing as the dependent variable,X₁ = % Attendance,X₂ = Salaries and X₃ = Spending.
The coefficient of multiple determination (R 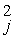 )of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below:
)of each of the 3 predictors with all the other remaining predictors are,respectively,0.0338,0.4669,and 0.4743.
The output from the best-subset regressions is given below:
 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):
 Model (II):
Model (II):
 Model (III):
Model (III):
 -Referring to Table 15-4,there is reason to suspect collinearity between some pairs of predictors.
-Referring to Table 15-4,there is reason to suspect collinearity between some pairs of predictors.
(True/False)
4.9/5  (33)
(33)
Showing 61 - 80 of 96
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)