Exam 5: Discrete Probability Distributions
Exam 1: An Introduction to Statistics44 Questions
Exam 2: Descriptive Statistics I: Elementary Data Presentation and Description147 Questions
Exam 3: Descriptive Statistics II: Additional Descriptive Measures and Data Displays128 Questions
Exam 4: Probability147 Questions
Exam 5: Discrete Probability Distributions144 Questions
Exam 6: Continuous Probability Distributions141 Questions
Exam 7: Statistical Inference: Estimating a Population Mean134 Questions
Exam 8: Interval Estimates for Proportions, Mean Differences and Proportion Differences19 Questions
Exam 9: Statistical Hypothesis Testing: Hypothesis Tests for a Population Mean62 Questions
Exam 10: Hypothesis Tests for Proportions, Mean Differences and Proportion Differences39 Questions
Exam 11: Basic Regression Analysis111 Questions
Exam 12: Multiple Regression53 Questions
Exam 13: F Tests and Analysis of Variance95 Questions
Exam 14: Experimental Designonline Only64 Questions
Exam 16: Chi-Square Tests145 Questions
Select questions type
Approximately 1% of all USPS package deliveries are lost.You select 10 deliveries at random.Assuming that all the binomial conditions are met, what is the "expected" number of lost packages in this 10 delivery sample?
(Multiple Choice)
4.9/5  (37)
(37)
The expected value of a discrete random variable is the average value for the random variable over many repeats of the experiment.
(True/False)
4.8/5  (27)
(27)
Use the Poisson probability function to find P(3 < x < 5), where λ = 2.
(Multiple Choice)
4.8/5  (39)
(39)
The following probability distribution represents the number of bedrooms in a randomly selected US household.To simplify matters, the category "five or more" is replaced by "5" (Source: US Census, American FactFinder).Calculate the variance of the number of bedrooms per household. 
(Multiple Choice)
4.8/5  (35)
(35)
Which of the following is a condition of a binomial experiment?
(Multiple Choice)
4.8/5  (32)
(32)
The expected value of a discrete random variable is the value of the random variable that occurs most frequently.
(True/False)
4.8/5  (42)
(42)
Which of the following best describes the logic of the binomial function?
(Multiple Choice)
4.8/5  (37)
(37)
Use the Poisson probability function to find P(x > 13), where λ = 5.
(Multiple Choice)
4.8/5  (28)
(28)
The symbol "x" is used to denote the random variable while the symbol "P(x)" is used to denote the probabilities associated with the random variable.
(True/False)
4.9/5  (44)
(44)
On average, 2.3 wind turbines at the vast Kindler Range Wind Farm malfunction and need repair.Assume that all the Poisson conditions are met.Letting x represent values of the random variable "number of turbines that malfunction during any one day," determine the probability that x = 2.
(Multiple Choice)
4.8/5  (37)
(37)
Use the Binomial distribution to produce P(x < 12), where n = 15, p = .7.
(Multiple Choice)
4.8/5  (37)
(37)
At work, Serge receives an average of four e-mails every hour.Assuming that all of the Poisson conditions are met, use the Poisson probability function to calculate the probability that Serge receives no e-mails in the next hour.
(Multiple Choice)
4.8/5  (20)
(20)
Car Sounds sells and installs high-end sound systems for cars.10% of the systems that the company installs need to be re-installed because of faulty first-time installation.You plan to randomly select 20 of Car Sounds' recent installations.How likely is it that the company will have to re-install no more than one of these systems?
(Multiple Choice)
4.9/5  (40)
(40)
Car Sounds sells and installs high-end sound systems for cars.10% of the systems that the company installs need to be re-installed because of faulty first-time installation.You plan to randomly select 20 of Car Sounds' recent installations.How likely is it that at least three of these systems will require re-installation.?
(Multiple Choice)
4.7/5  (33)
(33)
The number of re-tweets of your Twitter tweets over the last ten days is shown below.If you pick a day at random, how likely is it that the number of re-tweets on that day is 2? 3, 1, 1, 0, 1, 1, 2, 2, 0, 2.
(Multiple Choice)
4.8/5  (36)
(36)
Hi-Plains Design is bidding on a project that will earn the company at least $650 million.The competitive bidding process will involve presenting the company's proposal to three successive review panels at the client company, all of which must approve the proposal for Hi-Plains bid to be successful.If the proposal is approved by the first panel, Hi-Plains will present the proposal to the next panel.If it is approved there, Hi-Plains will present the proposal to the third panel.Hi-Plains estimates that its proposal has a 40% chance of approval at each of the stages.Define "number of Hi-Plains presentations" as your random variable for this "experiment." The possible values for the random variable (in ascending order) are:
(Multiple Choice)
4.9/5  (35)
(35)
The following probability distribution represents the number of vehicles available for use by a randomly selected US household.To simplify matters, the category "three or more" is replaced by "3" (Source: US Census, American FactFinder).Calculate the standard deviation of the number of vehicles available per household. 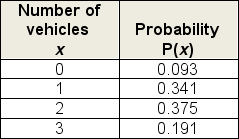
(Multiple Choice)
4.8/5  (37)
(37)
For a binomial distribution, find P(x = 2), where n = 8, p = .7.
(Multiple Choice)
4.8/5  (33)
(33)
Hi-Plains Design is bidding on a project that will earn the company at least $650 million.The competitive bidding process will involve presenting the company's proposal to three successive review panels at the client company, all of which must approve the proposal for Hi-Plains' bid to be successful.If the proposal is approved by the first panel, Hi-Plains will present the proposal to the next panel.If it is approved there, Hi-Plains will present the proposal to the third panel.Hi-Plains estimates that its proposal has a 40% chance of approval at each of the stages.Define "number of panels that fail to approve the proposal" as your random variable.The possible values for the random variable (in ascending order) are:
(Multiple Choice)
4.9/5  (40)
(40)
Showing 21 - 40 of 144
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)