Exam 3: Differentiation
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
A point is moving along the graph of the function 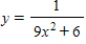 such that
such that 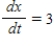 centimeters per second. Find
centimeters per second. Find 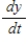 when
when 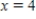 .
.
(Multiple Choice)
4.7/5  (33)
(33)
Evaluate 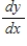 for the equation
for the equation 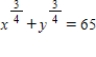 at the given point
at the given point 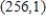 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (44)
(44)
Find an equation of the line that is tangent to the graph of the function 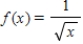 and parallel to the line
and parallel to the line 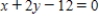 .
.
(Multiple Choice)
4.9/5  (39)
(39)
The radius, r, of a circle is decreasing at a rate of 2 centimeters per minute.
Find the rate of change of area, A, when the radius is 3.
(Multiple Choice)
4.8/5  (30)
(30)
Suppose the position function for a free-falling object on a certain planet is given by 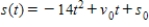 . A silver coin is dropped from the top of a building that is 1,366 feet tall. Find the time required for the coin to reach ground level. Round your answer to the three decimal places.
. A silver coin is dropped from the top of a building that is 1,366 feet tall. Find the time required for the coin to reach ground level. Round your answer to the three decimal places.
(Multiple Choice)
4.8/5  (29)
(29)
A petrol car is parked 50 feet from a long warehouse (see figure). The revolving light on top of the car turns at a rate of 30 revolutions per minute. How fast is the light beam moving along the wall when the beam makes an angle of 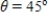 with the perpendicular from the light to the wall.
with the perpendicular from the light to the wall. 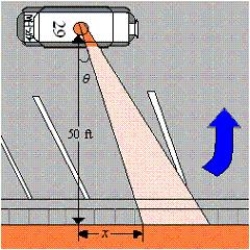
(Multiple Choice)
4.8/5  (36)
(36)
Suppose the position function for a free-falling object on a certain planet is given by 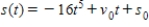 . A silver coin is dropped from the top of a building that is 1,372 feet tall. Determine the velocity function for the coin.
. A silver coin is dropped from the top of a building that is 1,372 feet tall. Determine the velocity function for the coin.
(Multiple Choice)
4.8/5  (44)
(44)
Approximate the zero(s) of the function. Use Newton's Method and continue the process until two successive approximations differ by less than 0.001. Round your answer to 5 decimal places. 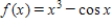 ,
, 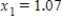
(Multiple Choice)
4.8/5  (31)
(31)
A ball is thrown straight down from the top of a 220-ft building with an initial velocity of -16 ft per second. The position function is 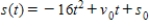 . What is the velocity of the ball after 4 seconds?
. What is the velocity of the ball after 4 seconds?
(Multiple Choice)
4.9/5  (38)
(38)
Given the derivative below find the requested higher-order derivative. 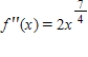 ,
, 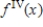 .
.
(Multiple Choice)
4.8/5  (43)
(43)
Showing 41 - 60 of 193
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)